复杂网络建模-课程笔记

对复杂网络的学习和入门，需要实践！

复杂网络基本内容
课程链接：https://www.bilibili.com/video/BV1WR4y1G7kH?p=3
基于Python+NetworkX的实现

课程的主要内容：

1、图论基础
2、复杂网络的统计特性
3、随机网络
4、小世界网络
5、无标度网络（重点介绍ba无标度网络）
6、网络鲁棒性
7、网络上的传播现象（疾病的网络传播动力学）
8、网络中的社团结构

课程的参考资料：

1、《巴拉巴西网络科学》，本课程强烈推荐
2、NetworkX的Document

常用的复杂网络构建工具：

Pejek、NetworkX、Igraph、Gephi

网络定义了各个组件之间的交互；
网络科学源于图论，但是两者并不等同：在图论中，需要开发抽象的数学工具；，以解析的方式来研究图，此时的研究对象是图；相反，在网络科学中，我们着重用建模的方式给出描述某种网络的特性，研究对象是网络；
网络往往表现出高度的复杂性，表现在网络机构的复杂性，网络节点的复杂性；网络演化过程（动力学）的复杂性。

网络中一些常见的统计策略（网络的基本静态几何特征）：

连接矩阵；
度，平均度，度分布；
最短路径长度；
集聚系数；（邻居节点之间的连接程度）。平均集聚系数。全局聚集系数；
网络的连通性；
度度相关性；（描述了度大的节点和度小节点之间的关系，若两者倾向连接则度度正相关，反之负相关），用来区分同配网络和异配网络的一个指标；还有基于pearson相关系数的度-度相关性；
网络的介数。有的节点虽然度很小但是属于两个社团的中间联系人，为了量化这样的节点，定义了一个关键的全局几何量——介数。介数分为节点介数，边介数。反应节点或者边在整个网络中的作用或者影响力；如何量化呢？可以用经过该节点的最短路径条数，比上两个节点间所有的最短路径条数。
网络的核度。一个图的k核，是反复去掉度值小于k的节点及其连线后，所剩余的子图，该子图的节点数就是该核的大小。如果一个节点属于k核，不属于k+1核，则此节点的核度为k。节点核度的最大值叫做网络的核度。k核可以用来描述度分布所不能描述的网络特征。
网络密度，指的是一个网络中各个节点之间联络的紧密程度。

几种常用的中心性指标：

度中心性；分为节点度中心性（一个节点在与之相连的邻居节点中的中心程度），和网络度中心性（一个节点在整个网络的中心程度）。这个指标用来表征整个网络的集中和集权程度。即整个网络围绕一个节点或者一组节点运行的程度。具体如何操作，对度值做归一化处理；
介数中心性，分为节点介数中心性和网络介数中心性；
接近度中心性；
特征向量中心性 -> Pagerank度中心性；

有向网络和加权网络的静态特征

入度，出度；
入度分布，出度分布；
平均距离和效率；
点权：与这个节点相连所有边的权重之和；
单位权：点权处于该节点的度值，得到单位权；
权重分布差异性：

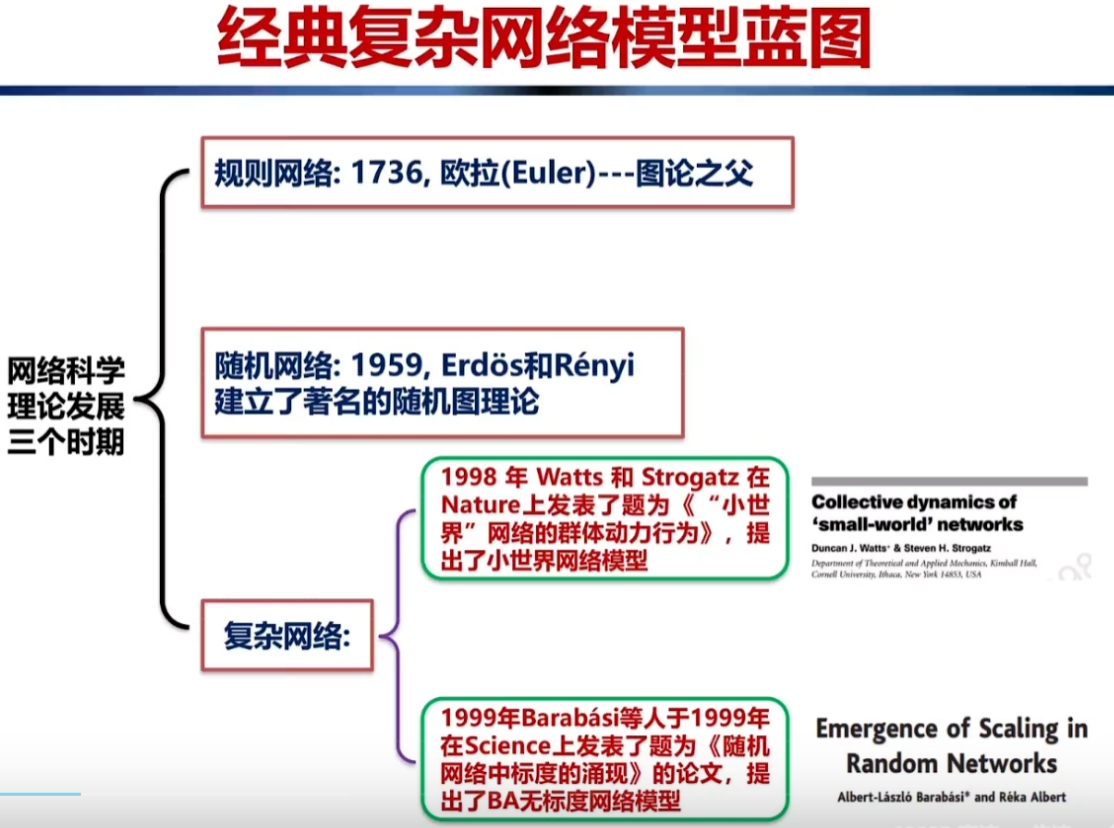
网络科学发展的三个时期：

1、规则网络，欧拉，1736年；
2、随机网络，两位匈牙利科学家，Erdos，Renyi，1959
3、复杂网络，Science，Nature上的两篇开山之作。1998,1999年。

规则网络

1、孤立节点网络；
2、全局耦合网络；
3、星型网络；
4、一维环；
5、二维晶格；

如何生成相应的网络

ER随机网络

1、众所周知，网络科学的目标是为了建立、再现真实网络特性的模型；

随机网络的两种生成方式：
1、G(N, l)模型；
2、G(N, p)模型；

ER随机网络的机构特性
1、期望连边数；
2、ER网络的平均距离和平均集聚系数；

总结：ER随机网络具有，度分布近似服从泊松分布、平均距离短、聚集系数小等性质；

ER随机网络的演化；

1、当平均度小于1时：亚临界，没有巨大的组件；
2、= 1时，临界；临界渗流概率，$ p_c = 1/N $
3、 > 1时，超临界；存在一个巨大连通组件；
4、 > lnN时，连通：生成的随机网络几乎是全连通的；

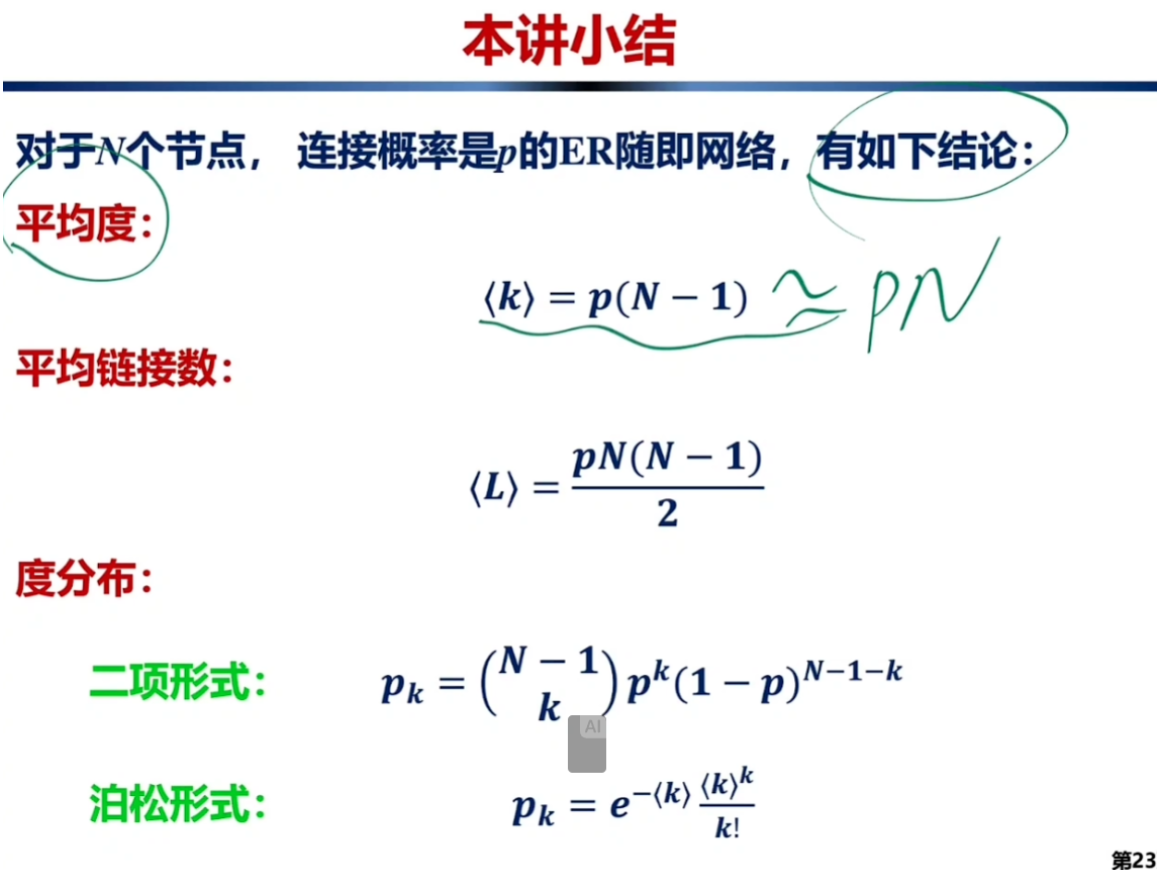
对ER随机网络的总结：

小世界网络

什么是小世界现象：六度分割；小世界现象意味着，随机选择两个节点之间的距离很短。
1、怎么算短？
2、如何解释短的现象？
小世界网络的定义是： $d_max = \frac{lnN}{ln}$

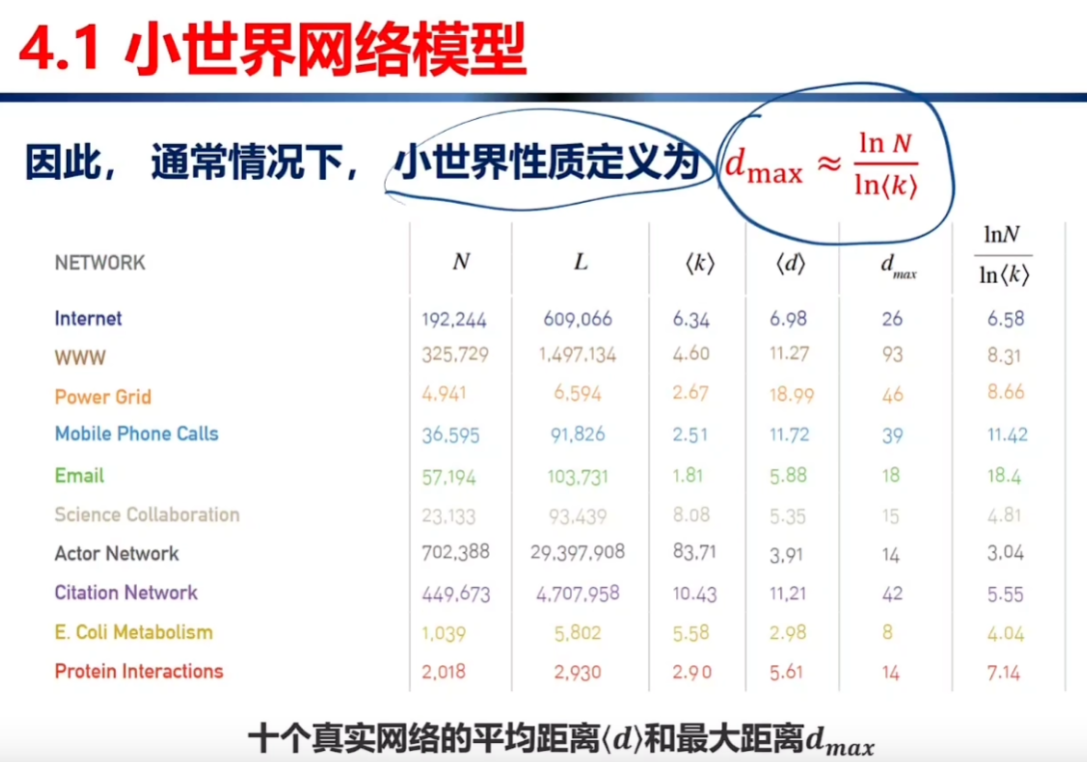
3、怎么算小？
小指的是，网络的平均路径长度或网络直径和网络大小的关系是对数关系。
即正比于lnN

小世界网络模型：
WS小世界网络模型；

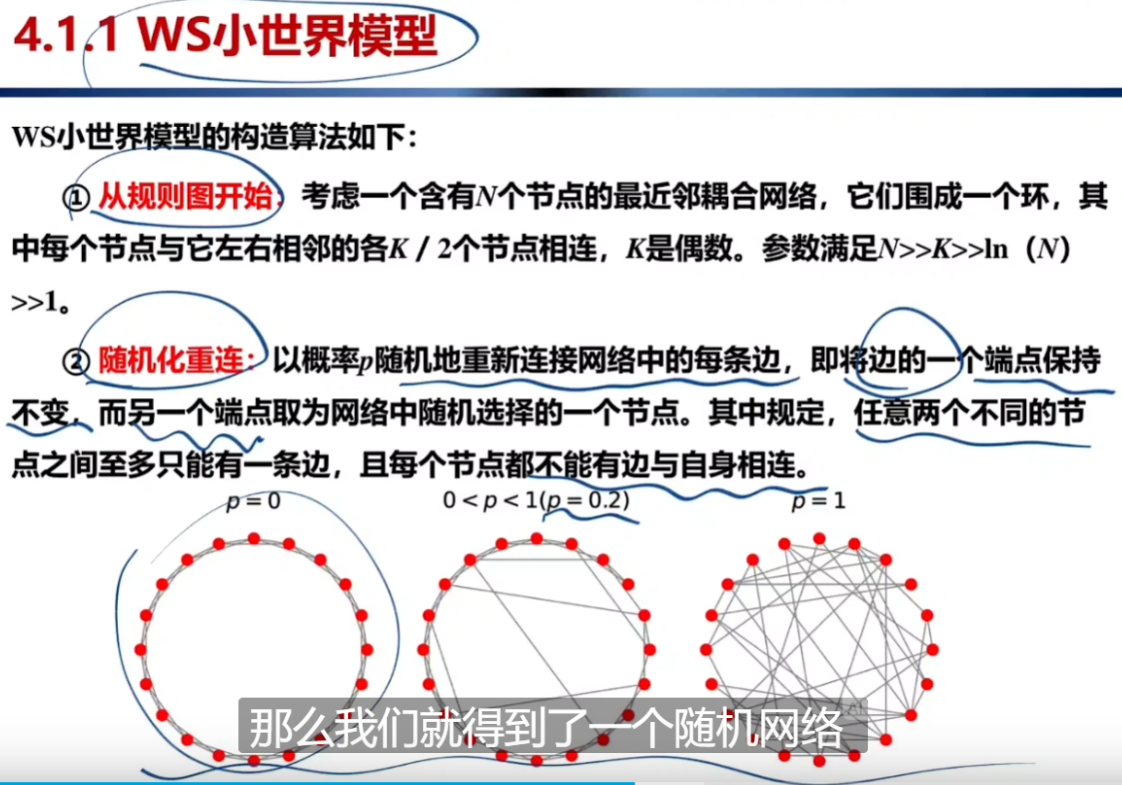
NW小世界网络模型：

除了上述两种生成小世界网络模型的方法外，还有很多其他种方法，比如加点，加边，去点，去边以及不同形式的交叉，等方法来产生小世界模型。

小世界网络的结构特性：
1、与ER随机图模型类似，WS小世界模型也是所有节点的度都近似相等的均匀网络；

https://www.bilibili.com/video/BV1WR4y1G7kH?p=26&t=165.6

2、目前对于小世界网络模型的平均距离，还有解析表达式，newman和watts利用重整化群的方法给出了一个近似表达式：
https://www.bilibili.com/video/BV1WR4y1G7kH?p=26&t=165.6

3、小世界网络的集聚系数；
有个结论：只要网络足够大，小世界行为在0 < p < 1范围内一定会出现；
https://www.bilibili.com/video/BV1WR4y1G7kH?p=26&t=165.6

关键结论：一方面，只要几条边的随机重连就足以减少网络的平均距离（有点进化论的味道）；另一方面，几条随机重连的边并不足以改变网络的局部集聚特性。

这类既具有较短的平均距离又具有较高的集聚系数的网络就是典型的小世界网络；

现实生活中的小世界网络和仿真的网络相比：平均路径长度差不太多，但是集聚系数差了好几个数量级。说明，真实世界中的集聚系数要远远大于随机网络的集聚系数。
https://www.bilibili.com/video/BV1WR4y1G7kH?p=26&t=165.6

真实网络中的集聚系数，显著地偏离随机网络的预测结果：
https://www.bilibili.com/video/BV1WR4y1G7kH?p=26&t=165.6

如何计算度和集聚系数之间的依赖关系？
https://www.bilibili.com/video/BV1WR4y1G7kH?p=26&t=165.6

对WS小世界网络的总结：
1、重连并不会改变网络的平均度；
2、连边的数量也不会发生变化；
3、度分布，近似泊松分布；
4、平均距离短；
5、集聚系数高；

无标度网络

无标度性质
1、什么是无标度呢？实际上是对网络度分布的一个描述；
2、枢纽节点标志着，真实网络中蕴含着一种比随机性更深层次的组织原则；即无标度性质；
3、离散和连续的幂率分布形式：

4、度分布服从幂率分布的网络，被称为无标度网络。
5、枢纽节点
6、随机网络和无标度网络的主要区别体现在度分布的尾部，在无标度网络中，大量小度节点和少量拥有很多链接的枢纽节点共存。

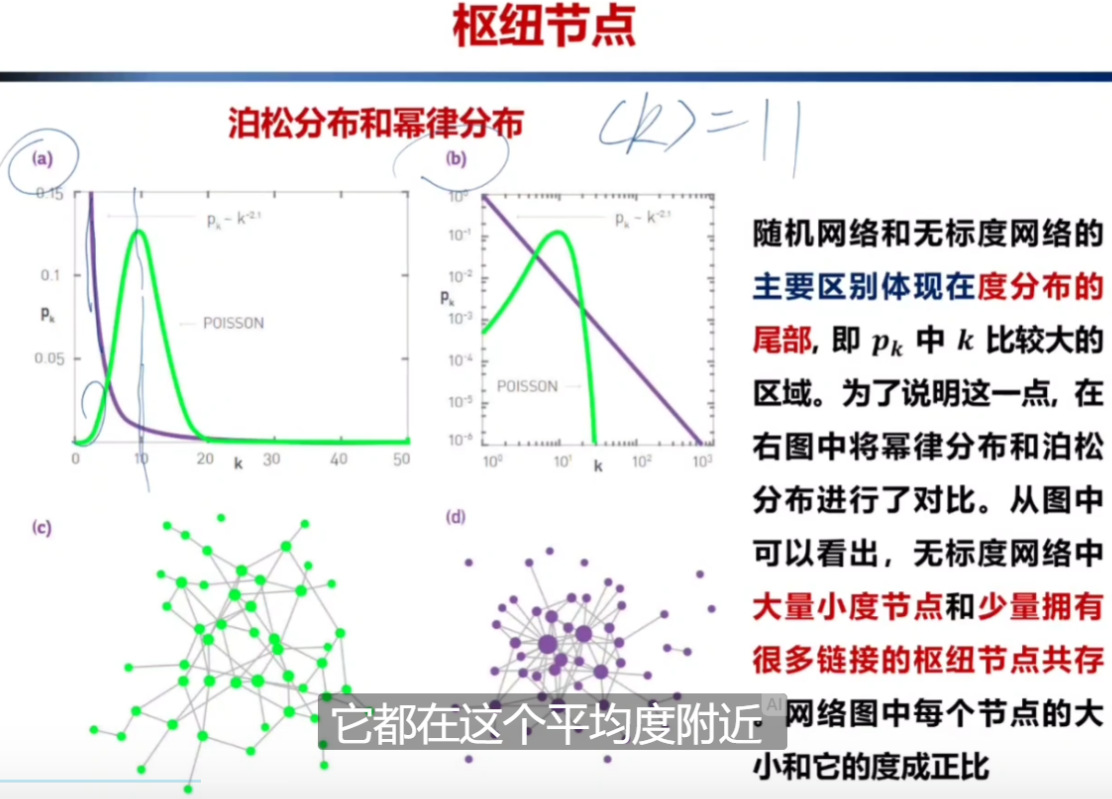
7、网络的大小，是如何影响枢纽的大小呢？
网络的最大度，
8、网络越大，其最大枢纽节点的度就越大，在大型无标度网络中，最大度和最小度之间可能相差几个数量级；
9、有趣的结论：枢纽节点在随机网络中不存在，在无标度网络中却自然出现。高速公路 v.s. 机场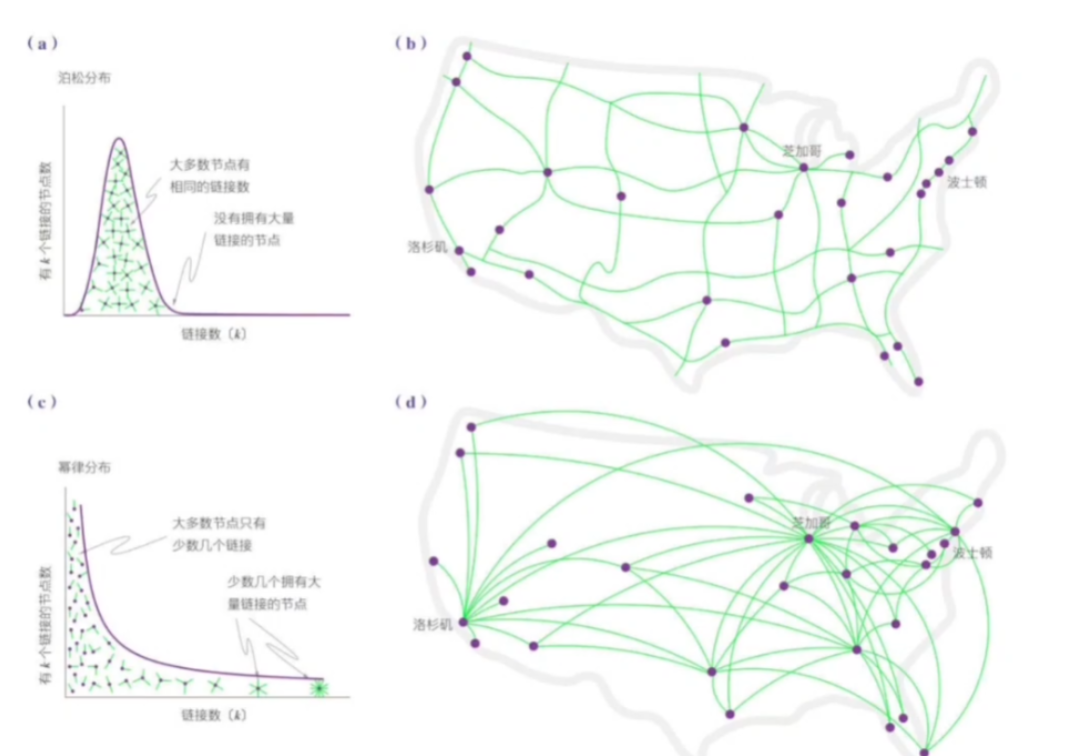

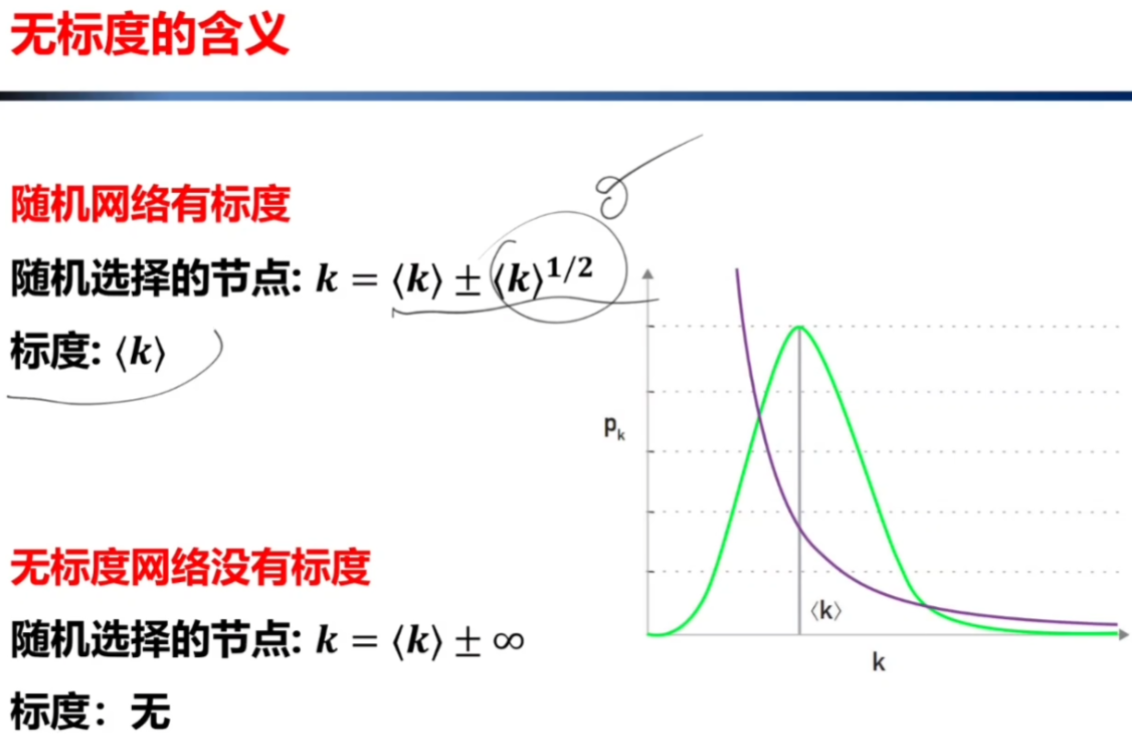
10、无标度的含义和超小世界性质：无标度这个词具体有什么含义？
（1）随机网络是有标度的，平均度k就可以作为随机网络的标度。
（2)无标度网络是没有标度，因为二阶矩就可能无限大。直白的理解就是，你不能通过计算平均值来表达这个群落的基本情况；总之，无标度的含义是，网络中节点的度相差很大，缺少一个内在的标度

11、如何知道一个网络是不是无标度网络？

（1）看一下度分布；

（2）测量，度指数；

（3）看看真实网络中P_k的形状；

（4）代码仿真


# 幂率分布：以BA无标度网络为例
n = 10000
m = 3
BA = nx.barabasi_albert_graph(n, m)
#获取网络的平均度
d = dict(nx.degree(BA))
print("平均度为:{}".format(sum(d.values())/len(d.keys())))

#获取所有度值对应的概率
x = list(range(max(d.values()) + 1))  #构造横坐标
y = [i/n for i in nx.degree_histogram(BA)]

#绘制度分布
fig, ax = plt.subplots()
ax.plot(x, y, 'ro-')
ax.set_xlabel('$k$', fontsize='large')
ax.set_ylabel('$p_k$', fontsize='large')
ax.legend(loc="best")
ax.set_title("degree distribution")
fig.show()
#fig.savefig('degree distribution.pdf')

#在双对数坐标系下，显示
#绘制度分布
newX = []
newY = []
for i in range(len(x)):
    if y[i] != 0 :
        newX.append(x[i])
        newY.append(y[i])

fig, ax = plt.subplots()
ax.plot(newX,newY, 'ro-')
ax.set_xscale("log")
ax.set_yscale("log")

ax.set_xlabel('$k$', fontsize='large')
ax.set_ylabel('$p_k$', fontsize='large')
ax.legend(loc="best")
ax.set_title("degree distribution")
fig.show()

结果如下：

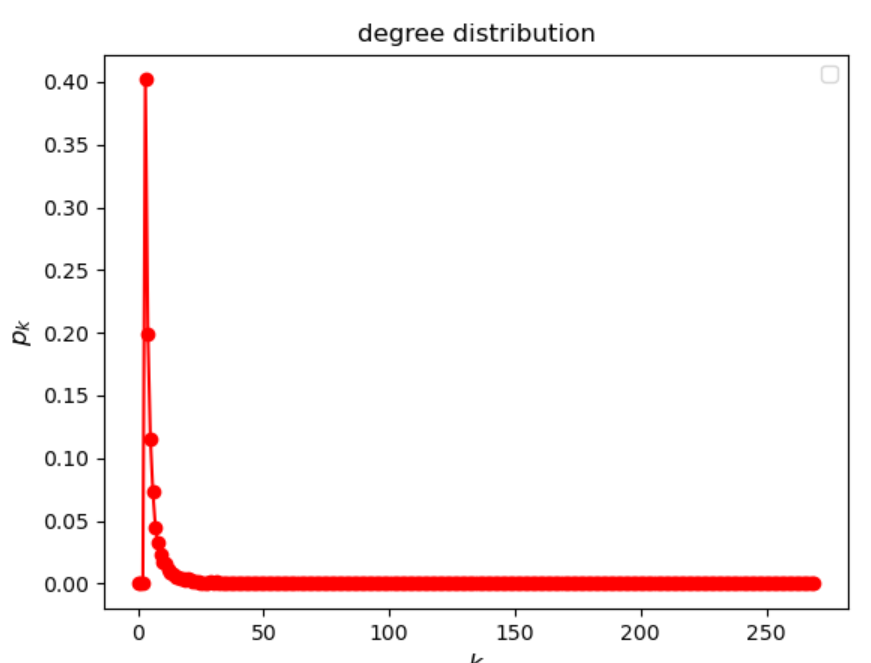
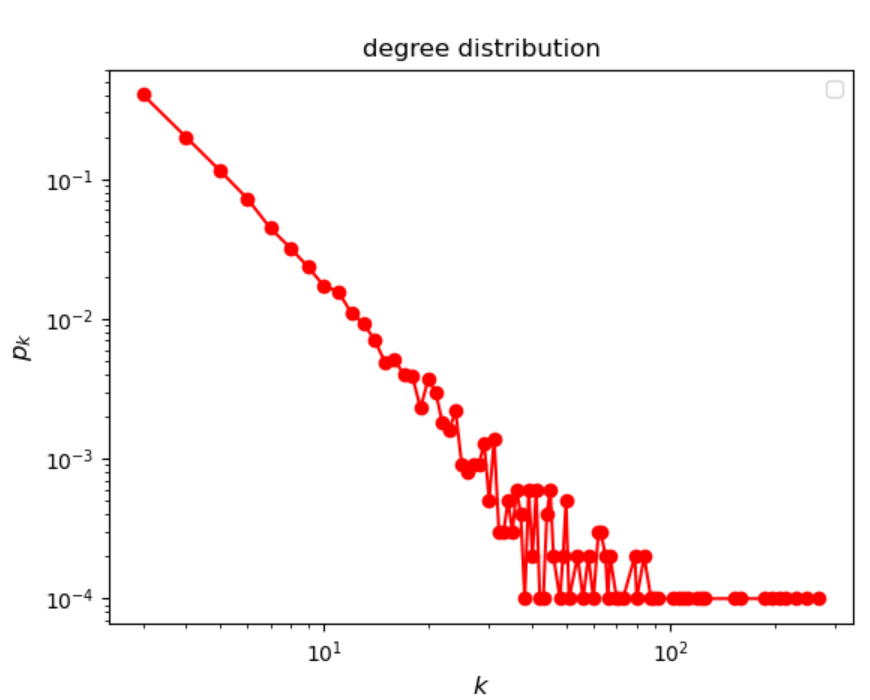
（5）如何估计幂率分布的，斜率呢？使用Python包，powerlaw

方案1：采用普通的估计方法：

from scipy import optimize
import numpy as np

#定义需要拟合的函数
def fit_line(x, a, b):
    return a*x + b

k, pk = get_dgreeDistr(BA)

kmin = np.min(k)
kmax = np.max(k)

x = np.log10(np.array(k))
y = np.log10(np.array(pk))

# 确定拟合的参数
a, b = optimize.curve_fit(fit_line, x, y)[0]

#有了拟合后的直线后，构造一条直线；
x1 = np.arange(kmin, kmax,0.1)
y1 = (10 ** b) * (x1 ** a)

fig, ax = plt.subplots()
ax.plot(k, pk, 'ro-')
ax.plot(x1, y1, 'b-')
ax.set_xlabel('$k$', fontsize='large')
ax.set_ylabel('$p_k$', fontsize='large')
ax.set_ylim(1e-4,1)
ax.set_xscale("log")
ax.set_yscale("log")
ax.legend(loc="best")
ax.set_title("fit")
fig.show()

结果如下：

方案2：

1	pip install powerlaw

import powerlaw
data = [BA.degree(i) for i in BA.nodes()]
print(max(data))

fit = powerlaw.Fit(data)
kmin = fit.power_law.xmin
alpha = fit.power_law.alpha
D = fit.power_law.D
print("kmin is {}".format(kmin))
print("gamma is {}".format(alpha))
print("kmin is {}".format(D))

fig, ax = plt.subplots()
ax = fit.plot_pdf(marker='o', color='b', linewidth=1)
fit.power_law.plot_pdf(color='b', linestyle='-',ax=ax)
fig.show()

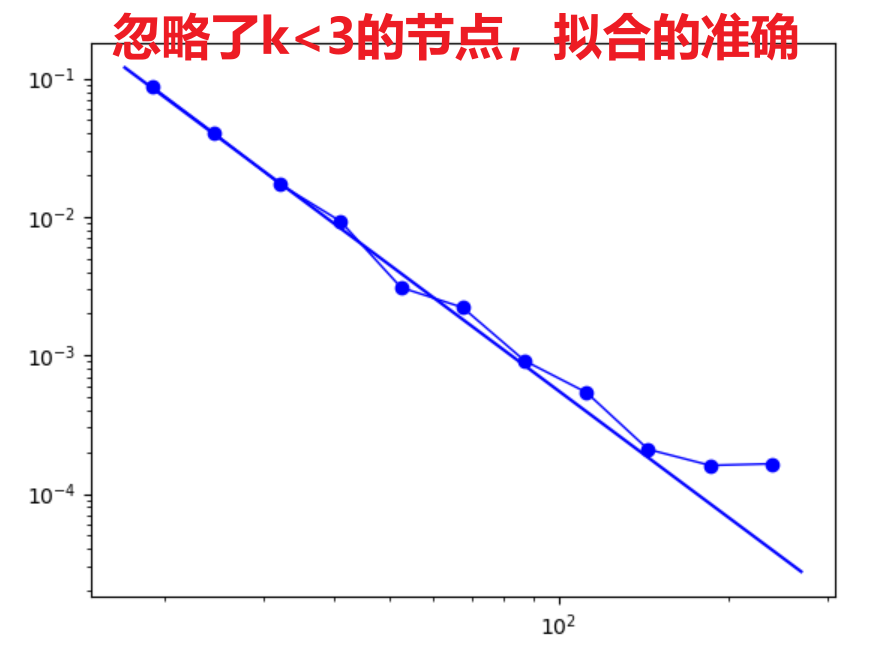
12、枢纽节点会影响小世界性质么？

重要结论：无标度网络中节点间的平均距离比随机网络中节点间的平均距离还要小；

13、无标度网络，度指数的作用：
（1）无标度网络和度指数\gamma相关，

有没有一种可能，把不同脑区神经元构成的网络的度分布对应的gama值，在gama坐标轴上进行体现呢？
（2)无标度网络的平均距离，超级小；

14、无标度网络的特性概述：
（1）度分布的两种形式：离散和连续；
（2）最大枢纽节点的度，要远远大于普通小度节点；
（3）当gamma介于2和3之间时，度的一阶矩是有限的，但是二阶矩是发散的；
（5）当gamma大于3时，度的一阶矩和二阶矩都是有限的；[随机网络]
（6）不同gamma值，对应的网络的平均距离满足此关系；
https://www.bilibili.com/video/BV1WR4y1G7kH?p=39&t=294.3

BA无标度网络

15、从icon网站上下载真实数据集

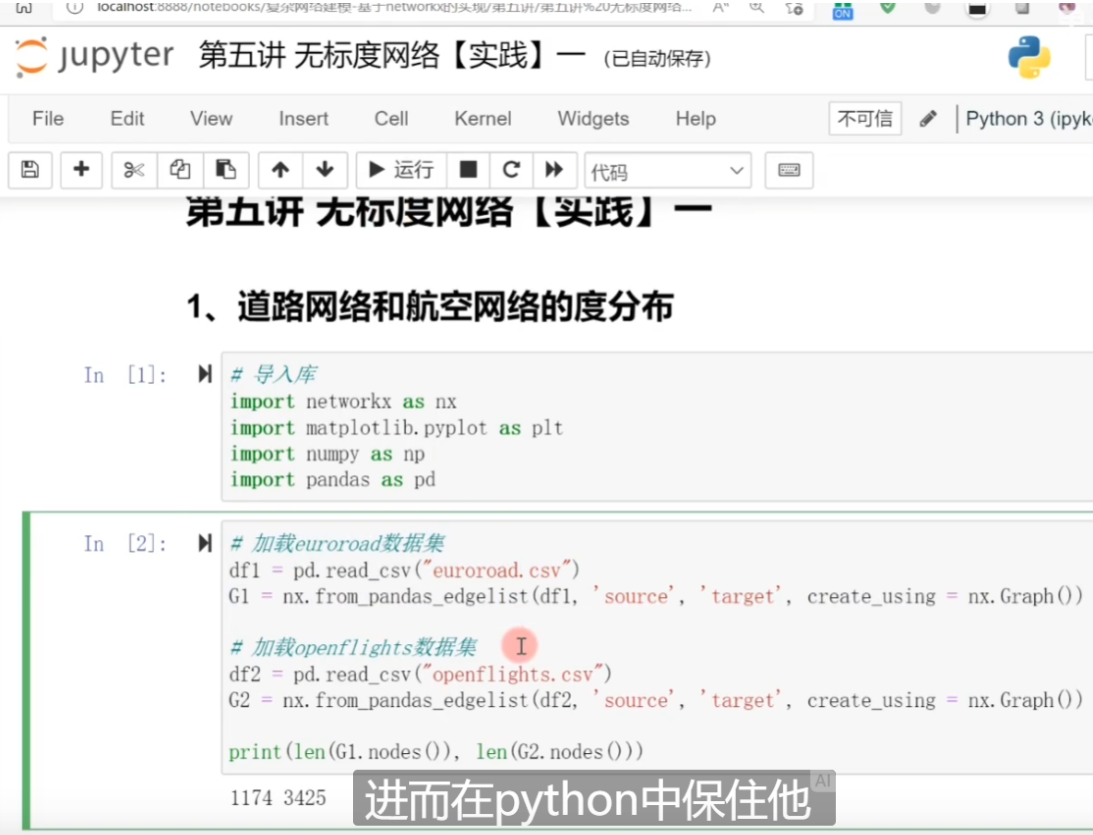
https://www.bilibili.com/video/BV1WR4y1G7kH?p=40&t=181.0

16、专门用来弥合幂率分布一个Python库 powerlaw
https://www.bilibili.com/video/BV1WR4y1G7kH?p=41&t=52.7

17、生成符合幂率分布的度序列：
https://www.bilibili.com/video/BV1WR4y1G7kH?p=42&t=0.7

18、利用配置模型，生成特定度分布指数的无标度网络：
https://www.bilibili.com/video/BV1WR4y1G7kH?p=43&t=5.2
（1）第一步，先生成一个满足幂率分布的度序列；
（2）利用此度序列，生成期望的无标度网络；
需要注意的是，
（1）配置模型包含了很多重连变，自环（但是这些在真实的环境中并不常见）；
（2）配置模型的平均度是不可控的；

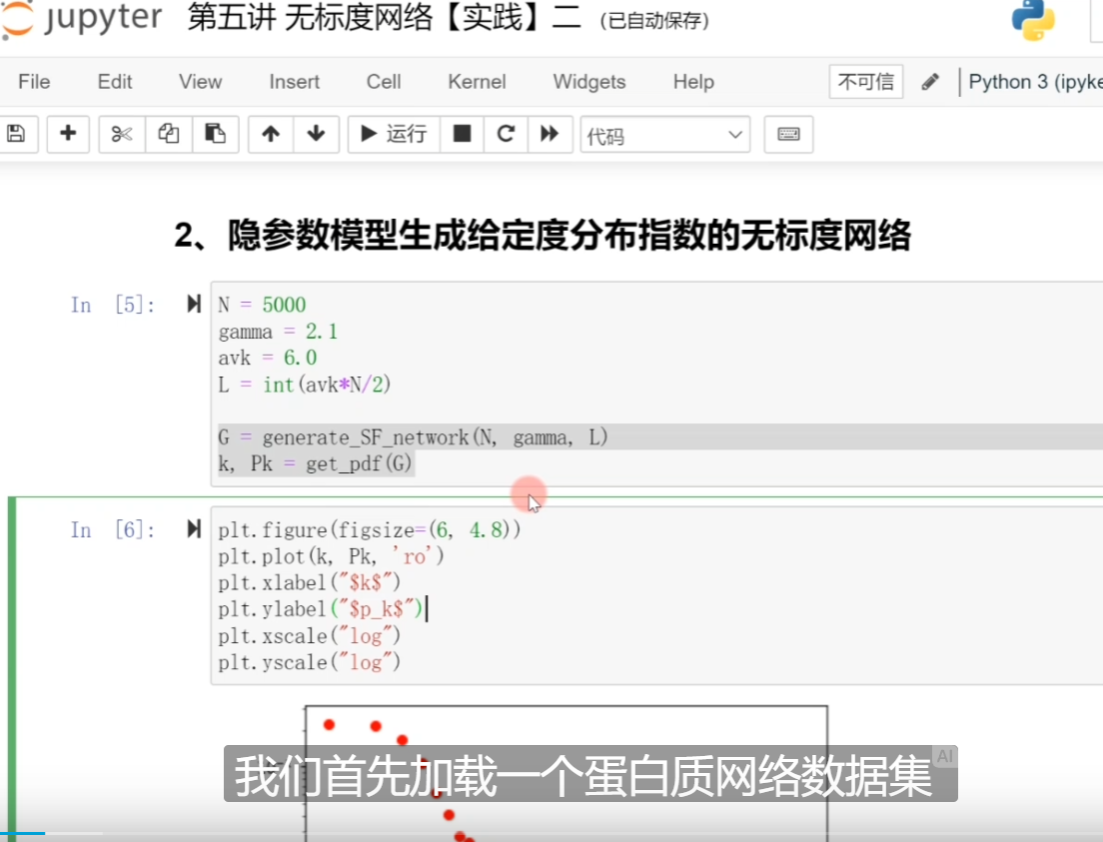
19、使用隐参数模型，生成给定度分布的无标度网络；
（1）不会产生自环
（2）不会产生多重连边；

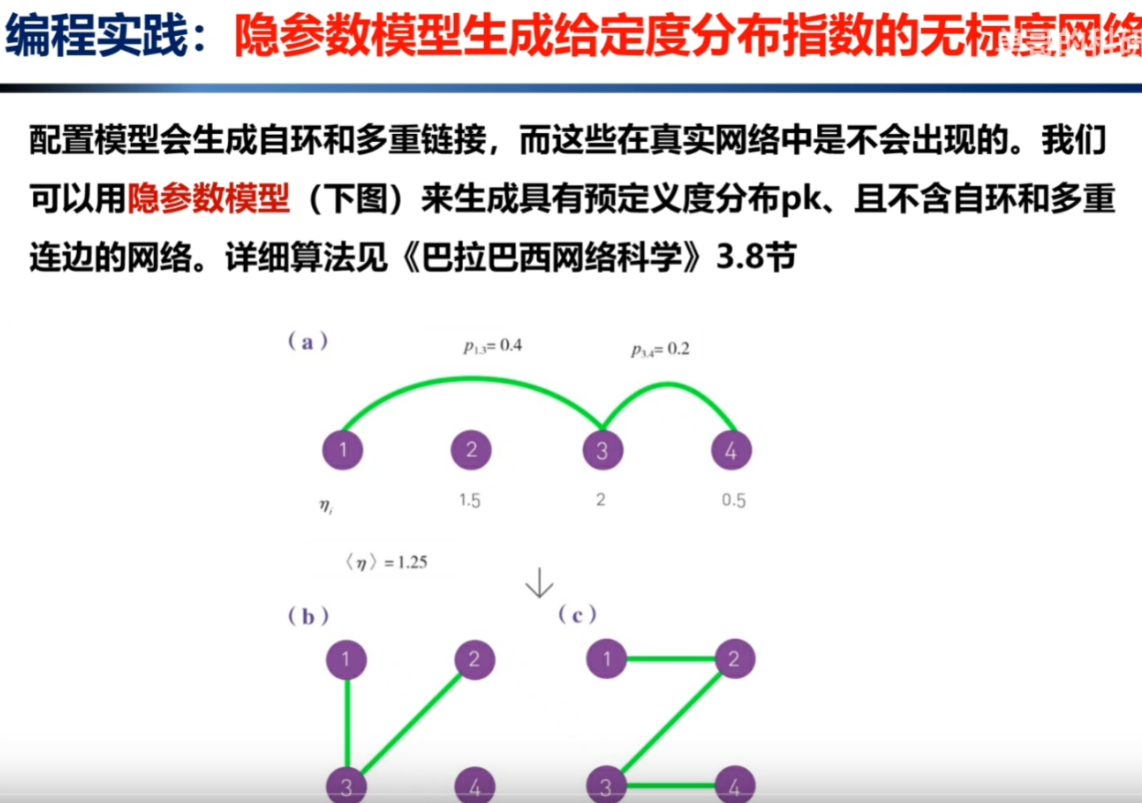
https://www.bilibili.com/video/BV1WR4y1G7kH?p=44&t=17.1

需要注意的是，隐参数模型也存在缺陷：
（1）只有当N，节点数很大时，生成的无标度网络才比较准确。

20、度保持的网络随机化
具体场景是：你手上有一个真实的网络模型，然后你想生成一个具有相同节点数和边数的随机模型，或者每个节点的度值一样，但是连接的方式不一样的随机网络，调用networkX的double_edge_swap()；
https://www.bilibili.com/video/BV1WR4y1G7kH?p=45&t=92.7

在研究过程中，选择一个合适的随机化方法是非常重要的；