学习这门课的初心是,希望了解非线性系统的分析和建模方法。
课程老师 北京工业大学 杨晓东!
课程链接:
https://www.bilibili.com/video/BV1KK411g7pj
第一节课
一个非常简单的非线性振动问题;
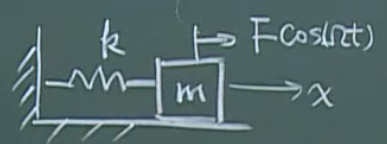
1、初始状态,偏离了x
那么在没有外力的情况下,
-kx = ma = mx’’ (a是加速度,是x位移的二阶导数)
即 -kx = mx’’ 这是个瞬态解;
对应x是个周期运动,瞬态解;
求解过程如上图;
但是如果施加一个周期力
Fcos(wt)
那么这部分的解对应的是稳态解;
原始视频在这里,讲的非常好;
2、重要的是,为什么摩擦力(阻尼)要跟x’ x的一阶导数(速度)相关呢?
阻尼
(1)如果和 x’’ 相关,就是和惯性相关,有关质量的,m。
(2)那么如果在运动的过程中,动的时候,有影响,不动的时候,就不展示的话,这个就是阻尼。
【c跟摩擦损耗,有速度的时候才有摩擦,没有速度的时候,就没有摩擦;】
(3)如果和 x 相关,那么就是和力,和变形,和刚性相关的;
【k是刚性,有位移的时候,才有弹性、刚性量,没有位移,没有没这一项。】
—
讲到这里,我单方面宣布,杨老师是我非线性动力学,振动的启蒙老师。我被吸引了。这个杨老师绝对是偶像,对问题的理解非常深入。
—
接下里进入双振子系统:

三个弹簧,两个质量块。这个问题属于线性的耦合问题。还没上升到非线性领域。为什么啊。因为(1)、不涉及时变,即k没有随时间变化、m没有随时间变化、(2)没有涉及到乘积、幂、三角函数。后边这个理由目前觉得稍微有点扯淡。
对于一个系统来说,在工程中,我们一般关心它的频率和模态问题。为什么?
因为,对于一个结构来说,我们关系的问题往往在它的共振上,如果外激励是已知的,剩下的问题,就是求解它的固有频率在哪?知道固有频率在哪,才知道他的控制频率在哪。这样才能避免共振点,或者利用共振点。
振动的同时性,由这样的数学形态进行描述的: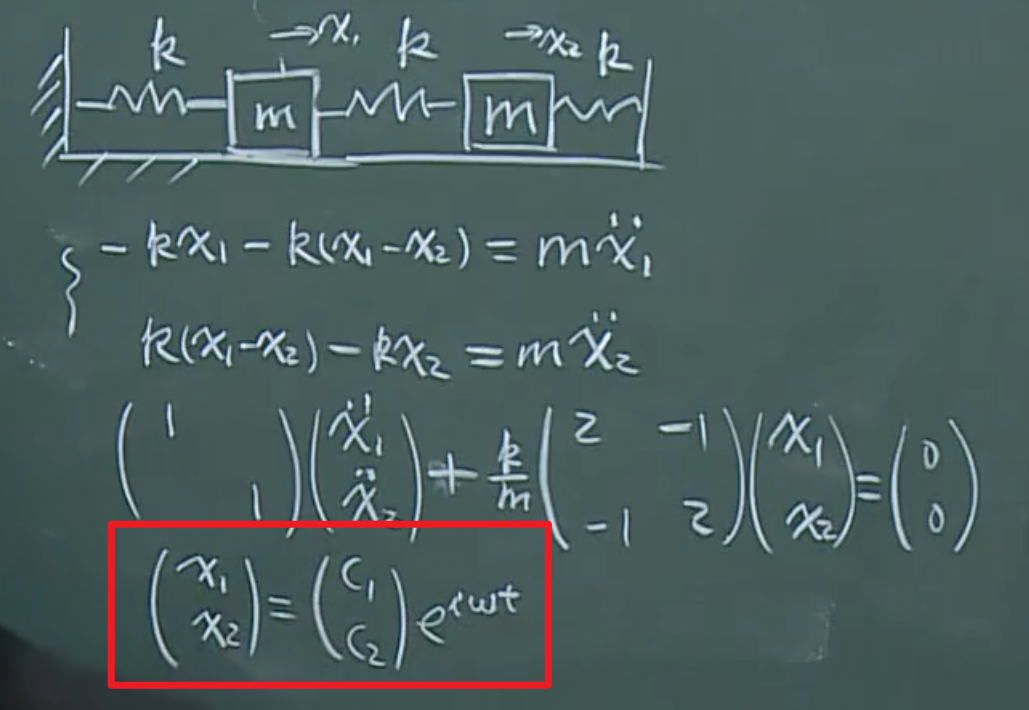
最后发现求解频率问题,实际上就是线性代数里边求解特征值问题。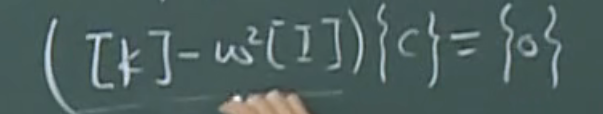
分析这个问题是复杂的,但是把这个问题的解写到两个模态上,瞬间解耦了。就是两个模态乘上系数再叠加。
这个振动是什么形式啊?是多个模态的叠加。为什么这样研究啊,不多个振子,一个振子一个振子的研究呢?原因是太麻烦了!这也体现了,模态分解的重要性;
广义左边的离散化。
https://www.bilibili.com/video/BV1KK411g7pj?t=1796.2
不管是自由运动,还是受迫振动,解决这类问题的方法都是一样的:
1、设解的形式;
2、直接把解的模态和频率求出来;相当于把方程做了一个解耦(这里是线性耦合)的处理;
3、然后就是模态的叠加;
看到非线性问题,首先,第一步,它的线性部分有没有解耦?非线性耦合往往叫做弱耦合;
N个方块,相当于N个自由度。它的频率该如何求解?
https://www.bilibili.com/video/BV1KK411g7pj?t=1963.1
工程中一般研究低频问题,很少研究高频问题。
单质点,两个自由度运动的问题: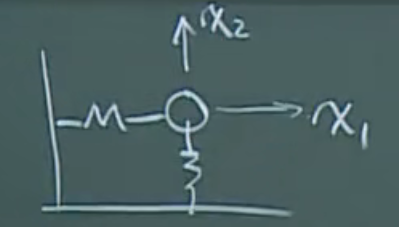
对于这个世界,如果我们想描述他的位移,有两种描述方式:
1、拉格朗日描述方法,随体的测量:如果想描述风扇叶片上下的运动,该怎么办?地面上,不行。因为页面跑了;如果完全捆绑到叶片上,也不行,因为上下运动都同步了。只能把激光放到和叶片一起旋转,未变形的刚性结构上。
2、欧拉描述方法:采用惯性空间的方法。大海的浪好高啊,这个所谓的浪高,并不是某个水分子有多高。而是那个地方的浪有多高。 欧拉描述方法应用到流体比较多的。
第二节课
https://www.bilibili.com/video/BV1KK411g7pj?p=2
梁的振动。
我们讲的振动和频率,是整体的频率,不是某个部位或者某个方向;
梁的轴向振动和横向振动,他们的频率比,差别非常之大;
高频往往不是我们关注的,低频往往是我们关注的。
准静态假设;
为什么要关注解析的方法,因为:
1、更宏观。更能把握住动力学特性的参数影响和变化;
如何求解模态和频率:
https://www.bilibili.com/video/BV1KK411g7pj?p=2&t=1562.9
模态和波要统一考虑
https://www.bilibili.com/video/BV1KK411g7pj?p=2&t=1762.5
没有边界就没有模态和频率;
不行了,第二节课是在扛不住了。