复杂神经动力学:分析与建模—从神经元脉冲到皮层震荡,从涌现到功能
讲座的视频来源:
https://www.bilibili.com/video/BV1mu411y7M4/?spm_id_from=333.788
目录
1、介绍:大脑作为多尺度复杂动态网络和功能系统;成本效益平衡;建模简介(Introduction: brain as multi-scale complex dynamical network and functional system; cost-efficiency trade-off; a brief overview of modeling)
从复杂系统的视角,把神经系统突出的结构和动力学特征做一个介绍。希望强调神经系统除了作为复杂系统外,还是功能系统,需要考虑成本和效益的均衡;然后对神经系统的建模做一个简要的综述;
2、在神经网络模型和平均场分析中协调不规则的神经元尖峰,神经雪崩和振荡(Reconcile irregular neuronal spiking, neural avalanches and oscilations in neural network model and mean-field analysis)
介绍单个神经元脉冲发放的动力学 和 神经回路出现的震荡、雪崩现象。怎么统一起来?用模型的研究方法,和 统计中平均场的方法 理解 涌现 的原理。
3、少即是多:神经回路动力学的成本效益(less is more:cost-effectiveness in neural circuit dynamics)
这样的动力学本质,实际上也满足了生物神经系统中 低成本来实现高效率的原理。
4、信息处理中的复杂神经动力学-学习和记忆补救(Complex neural dynamics in information processing- learning and memory rescue)
复杂的神经动力学,在局部的复杂网络中;结合外界的刺激、神经可塑性。来了解神经动力学,对信息处理(学习和记忆)的作用
5、在意识恢复过程中复杂的皮层波的传播(complex cortical propagation waves during the recovery of consciousness)
在皮层大尺度的框架下,了解神经动力学,在空间中表现出来波的传播。小鼠从麻醉到清醒的过程中,动力学特征的变化。可以用一些神经场的模型,来了解局部动力学(如连接的相互作用),为理解意识的恢复有一定的帮助。
6、大规模功能连接:层级模块化组织、多样性、平衡性和认知能力(Large-scale functional connectivity : hierarchical modular organization, diversity, balance and cognitive ability)
进入更大的尺度,人类大脑全脑的功能连接,结构连接,体现出来,大脑多层次、模块化的结构、跟功能的分离和整合。
大脑结构和功能的连接,体现出来的多层次模块化结构来支撑我们的大脑实现:记忆、功能、个体差异、认知能力的差别。
7、Model of neural computing from machine learning(机器学习的神经计算模型)
通过机器学习来构建模型,来实现动物上类似的的功能。还可以反过来,通过分析模型里边的结构和动力学 来理解生物系统底层实现计算的原理
8、总结(Summary and Outlooks) 和展望

收获 & 思考:
背景介绍:
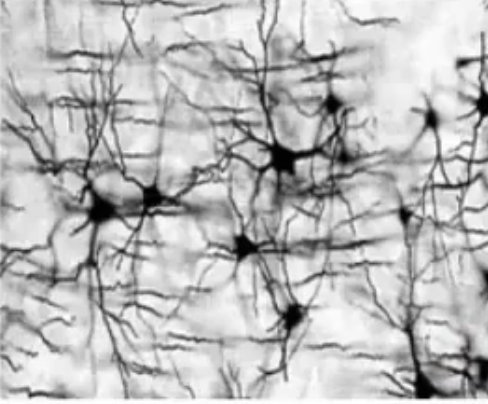
1、神经元,在小尺度上会形成局部的回路,如下图
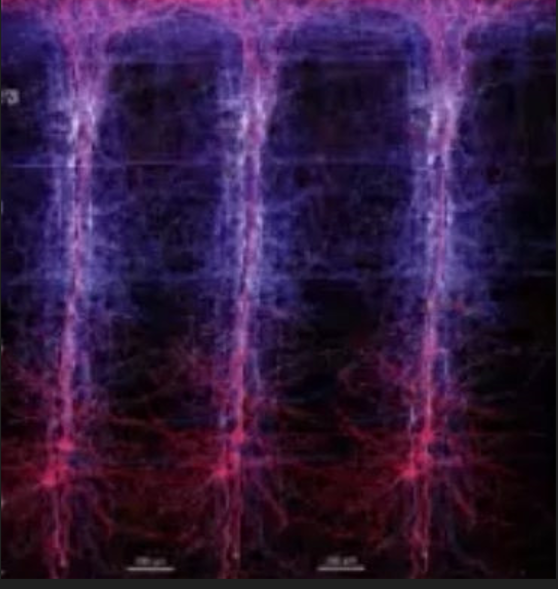
2、在大尺度上,还会形成皮层柱,如下图:
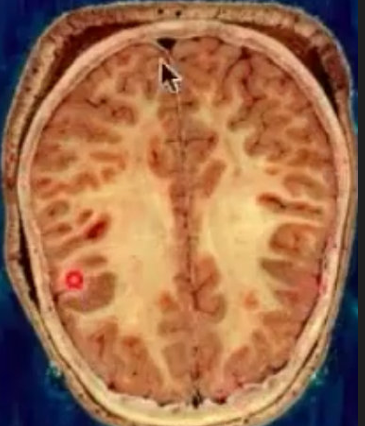
3、神经元局部的回路在大尺度上看就是 大脑中的绘制。而轴突而是白质,类似与大脑中的高速公路,如下图
4、成年人大脑中大概有860亿神经元。每个神经元有成千上万个突触。大脑占2%的体重,但是消耗人体的20%的能量(~20W左右)。非常高效的组织;
5、大脑背后的复杂系统跨越了多个空间和时间尺度:时间上,还包括了毫秒级别的分子动力学;
6、动物相比人来说,可以进行有创的成像;
7、大脑最大的特点是,大脑一直有自发的活动;
8、有一种说法:这种复杂的自发动力学,消耗了大脑大概95%的能量;引出来一个问题:伴随着生物进化,为什么大脑要花费这么多能量在这种动力学行为上,这些行为好像又没有直接进行处理过程。反过来讲,这种复杂的动力学行为,一定有很重要的价值和意义;
9、这种大脑自发的动力学行为,随着我们衰老、成长、甚至脑部疾病 会发生变化;
10、消耗了这么多能量,有很多代谢物质,这种代谢物质的堆积跟大脑很多的退行性病变都是息息相关的;
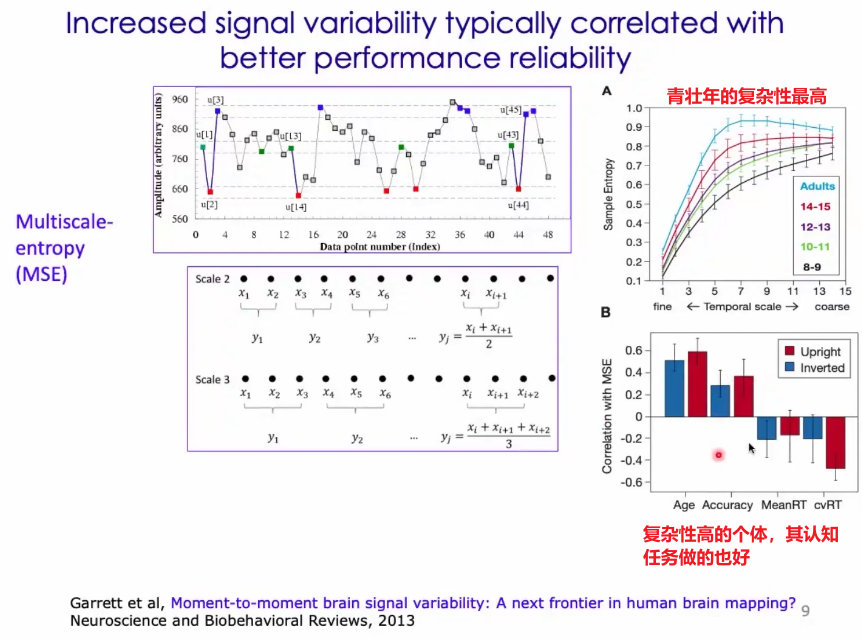
11、发育的过程中,随着大脑的复杂性发生变化时,人们的行为和认知也会发生变化;人青壮年的时候,神经系统的复杂性是最高的,同时人的能力也是最高的;
12、可以利用信息论中,熵的概念来刻画复杂性。很多生物信号,如果你用不同尺度的时间窗进行平均,你还是能看到它是在几个不同状态下连续波动的;这属于多尺度熵;
13、长久以来,研究者们往往把神经元的复杂性当做随机和噪声。ERP(event related potential)这种分析方法在某种程度上是为了降低信号的复杂性(即研究者眼中的噪声);实际上,我们要勇敢一些,面对复杂性、探索和利用复杂性!

14、神经元的电活动,是一个非常典型的非线性活动:
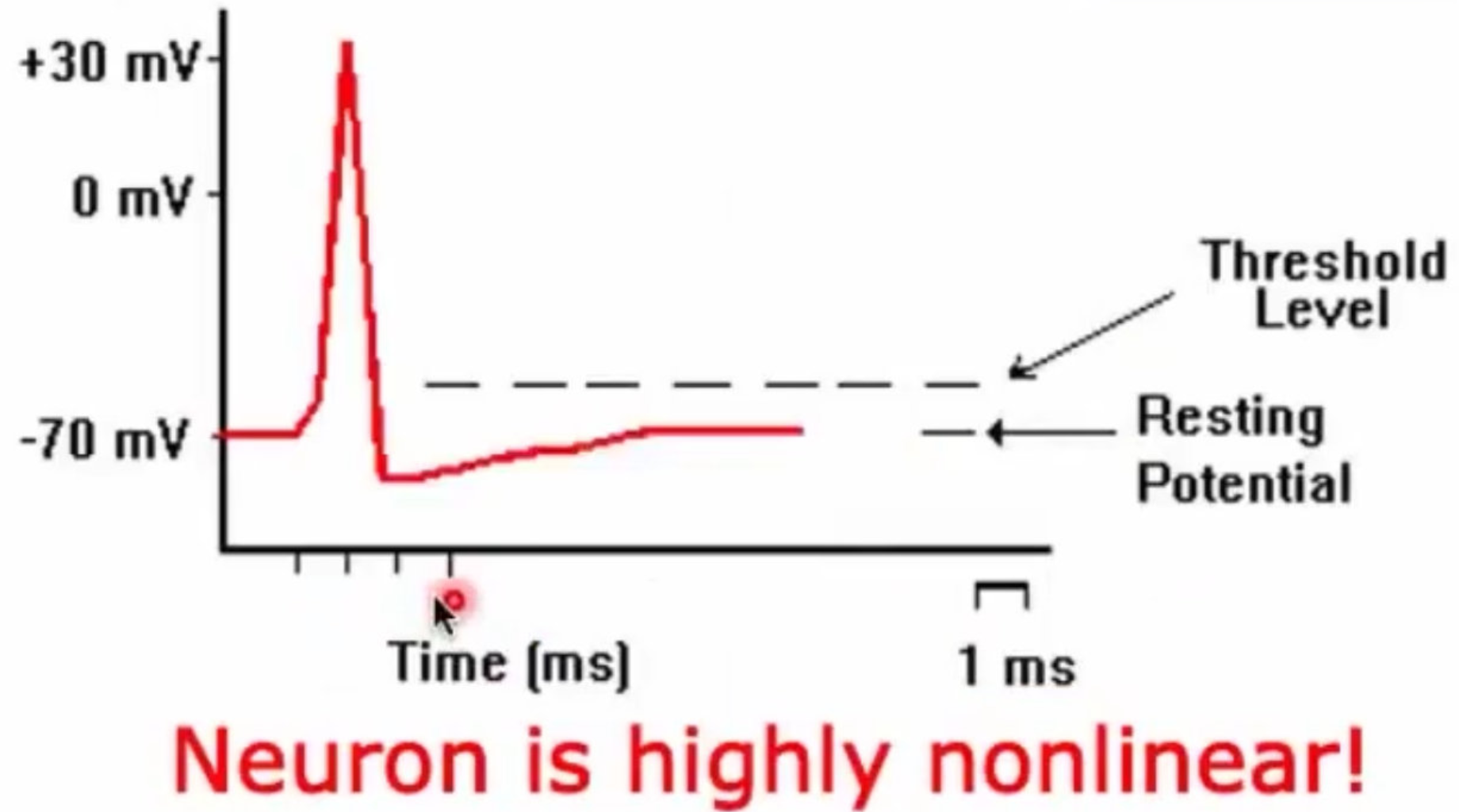
15、大脑不均匀、模块化、多层次的连接非常多;
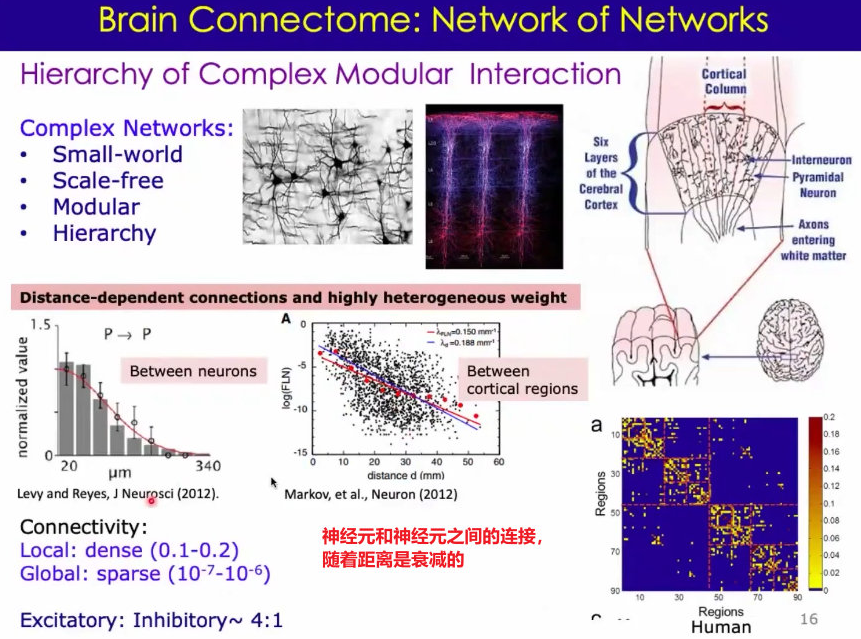
16、复杂系统在物理科学中有着基本的特征:组成单元有着非常强的非线性、有很多单元耦合起来;出现:混沌、自组织(Self-Organized Criticality, SOC)、涌现(emergence)这些行为;只观察单个单元,很难理解整个集群的行为; 迫切要求我们在系统层面观察、了解神经系统。
17、神经动力学在不同尺度上的一些突出的特征:(1)单个神经元层面:低发放率、无规则;(2)集群层面:簇放电(cluster firing)/神经元雪崩现象(neuronal avalanches)、网络震荡(非周期、多时间尺度)、皮层上波的传播;
18、特定任务下,神经元的发放是不重复的;
19、神经元的发放间隔服从泊松分布,意味着随机过程;
20、为什么会出现这种无规则的发放?(模型问题、理论问题为什么如此重要?) 引出,“平衡问题”的重要性!
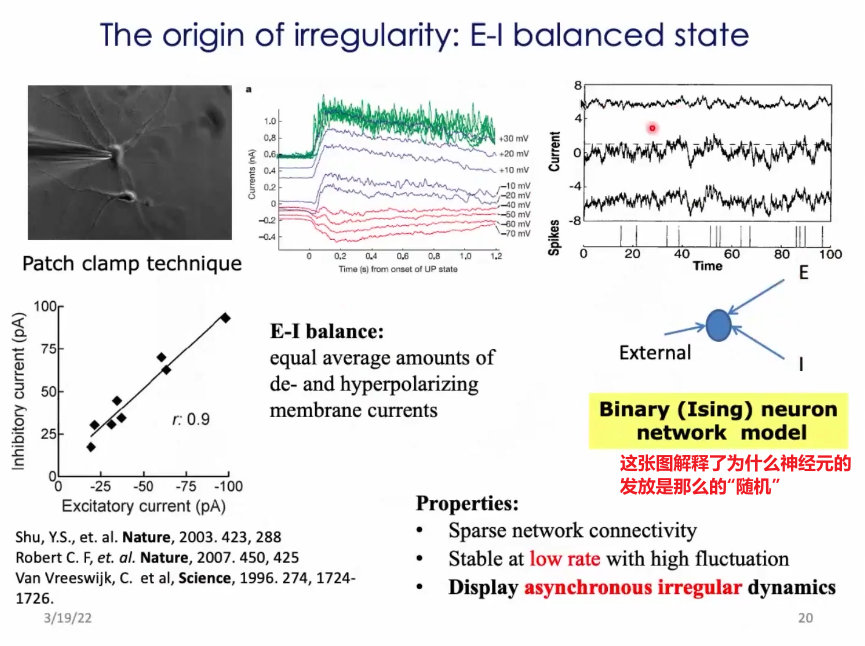
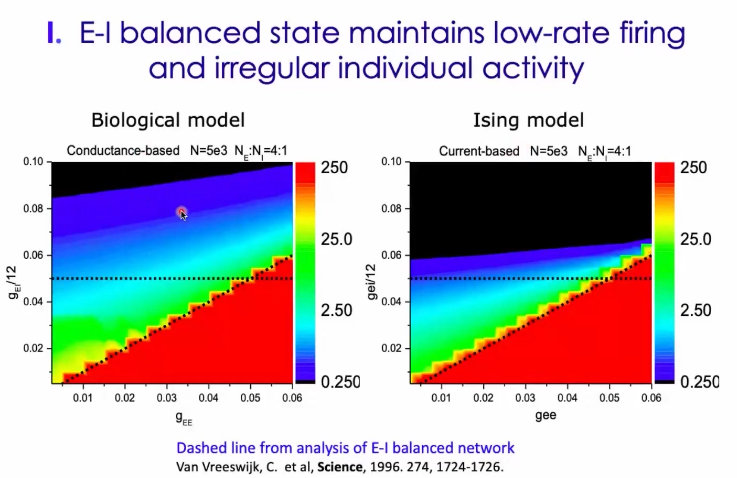
21、模型:每个神经元接收激活和抑制信号。如果两者相当,则神经元表现出无规则的随机信号特征。当两方其中一方实力过大时,超过神经元发放的阈值,进而导致神经元产生随机的发放;
22、Ising 模型:神经元网络是稀疏连接的(为什么要稀疏?稀疏之后,两个神经元没有相同的邻居,那么他们的输入是独立的;神经元之间相对是独立的;)、低发放率的。
23、E-I balance模型(神经元之间相互独立),能够实现:网络的发放率随着刺激的强弱呈现线性变化。而且平衡的时候,属于线性变化;线性模型没有太大意义,就像照镜子一样,没有新的东西。但这种模型在构建的时候用到了热力学极限,代价是很大的。
24、神经系统中的神经元,通过什么样的形式 group在一起呢?社会中的人, 有独立性、分工、合作。
25、两个神经元的电流,有相差,有时间窗。
26、 通过大尺度的成像方法, 你会发现神经元的发放并不是完全随机的;存在同步发放的结构,也叫做cluster。统计cluster 发放的概率,你会发现并不低;shuffle后的神经元,这种同步发放的概率非常低;
27、领域内一般认为,神经元对之间的相关性(对相关 pairse-correlation)超过0.3,才存在连接,如果只有0.01这种水平,就认为没有连接;
28、视野内大多数神经元同步发放的现象,在动力学系统中叫做雪崩。
29、随着神经元数量的显著性增加,会发现雪崩现象(cluster firing)的发生频率并不低;两者之间的关系服从幂率分布(也就是无标度分布);
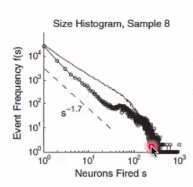
30、场电位反应的是,神经元集群的发放和活动;
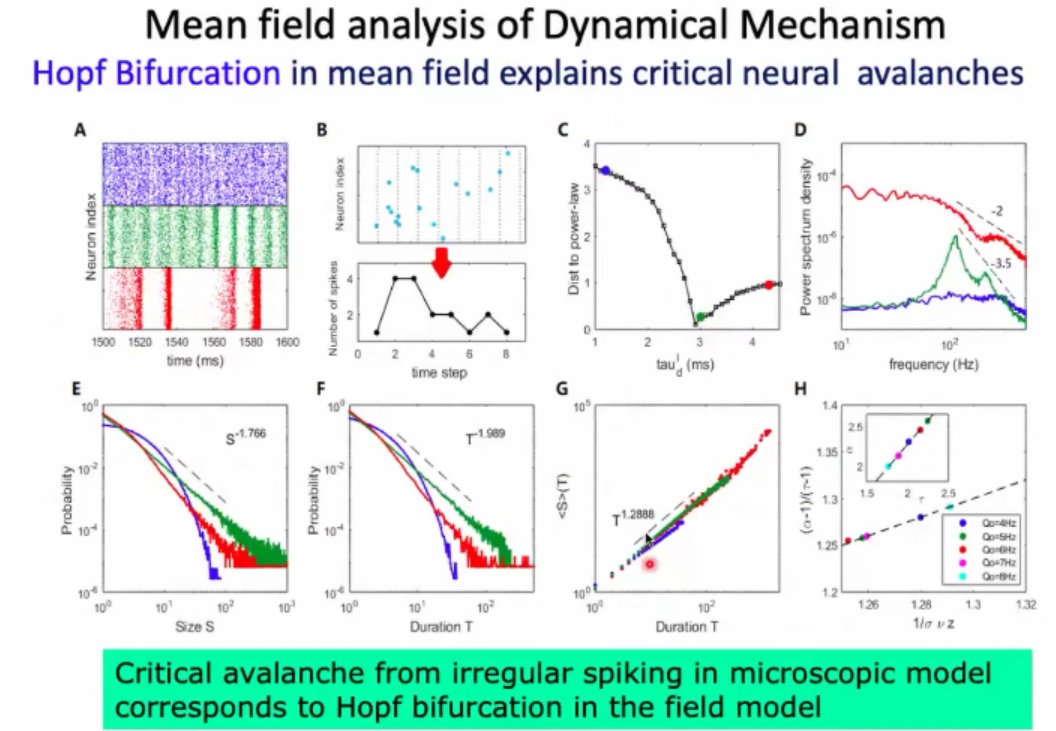
31、雪崩的形成,在皮层层面也是能观察到的。雪崩的数据分析方法:在视场中,设置某个阈值,然后可以看到大于该阈值的活动,在视野中是怎么扩散的。然后统计其雪崩的大小,结论如下:从麻醉到清醒的过程中,可以看到,在麻醉时(类似与睡眠)存在慢波,全脑有比较好的同步,会出现比较大的节律活动,但节律也比较慢;在清醒的时候,就不会出现大的节律活动,会表现出来很好的幂率,临界行为; (横坐标是雪崩pixel的数量,纵坐标是概率)
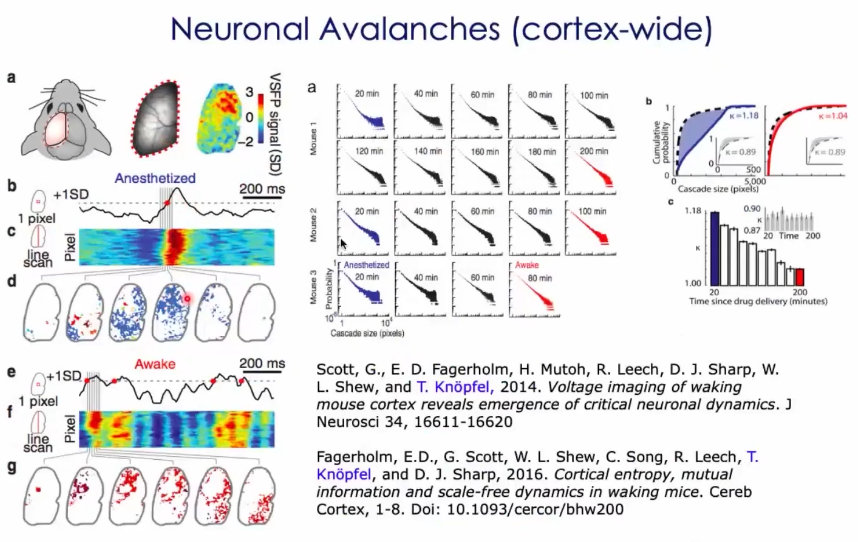
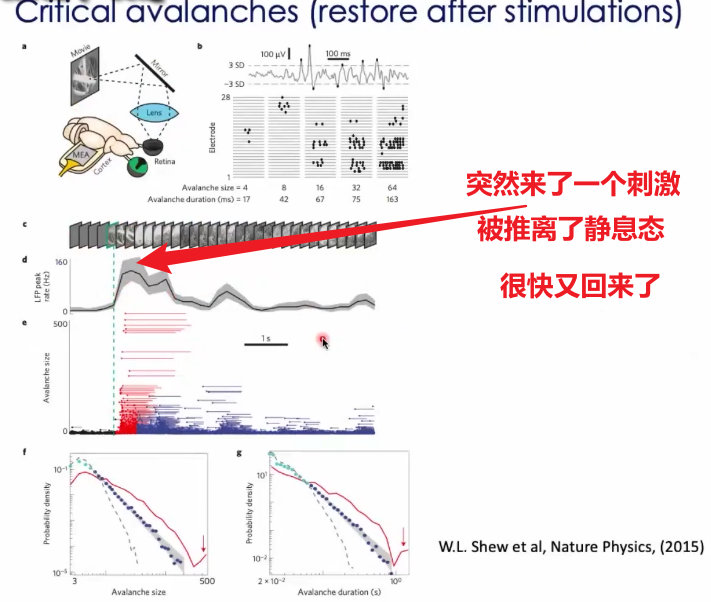
32、任务刺激后,神经元系统会很快从幂率分布的临界状态,被推离开。但是很快,又回到临界状态;结论:幂率这样的一种特征,是大脑在静息或者任务处理下,的一种基本特征。
33、 在fMR数据中,也能利用雪崩这种的数据分析方法。团簇的大小也服从幂率分布;
34、结论:从小鼠的局部网路到,到大脑的全局网络中,都存在幂率这样的平衡态。
35、在统计物理中,幂率分布和 临界性 、相变是相关的;物理中,需要人手工细调这个临界参数。拿大脑和物理系统中的临界状态类比,不同之处在于大脑不需要细调这样的参数,可以叫自组织临界行为。它自组织地靠近在临界态附近;
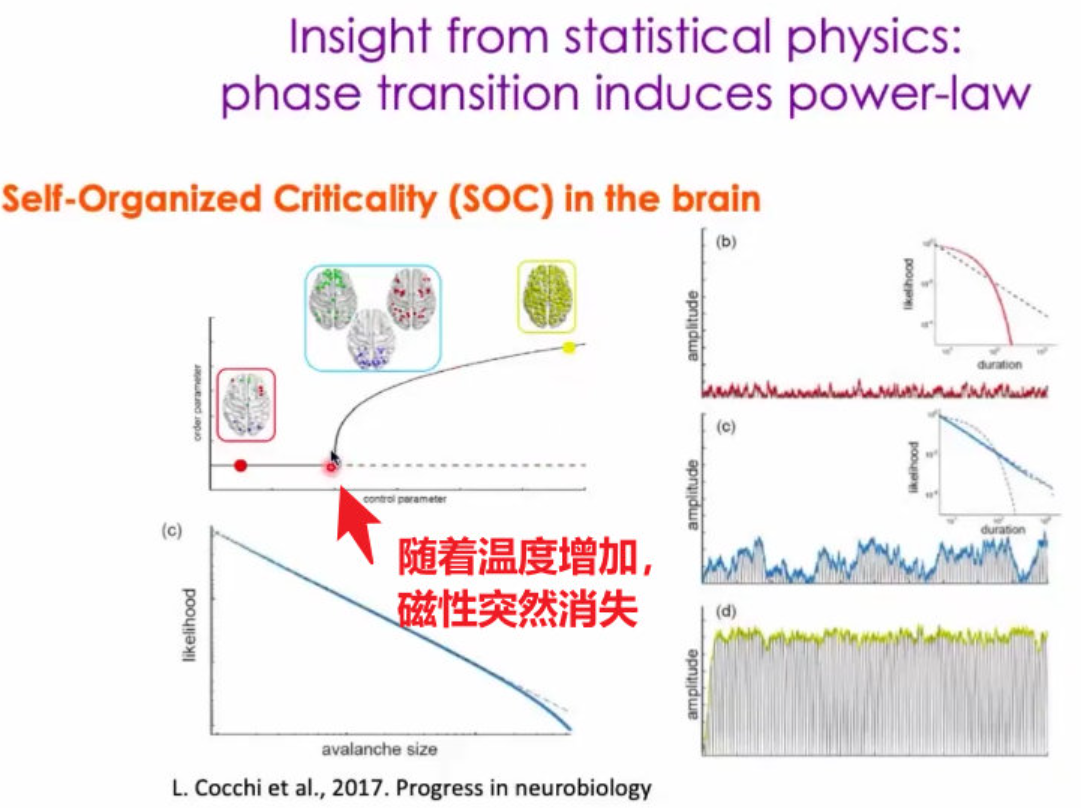
36、培养皿的实验证明,当神经网络偏离临界态后,对外界的药物或者其他刺激就不太敏感了。
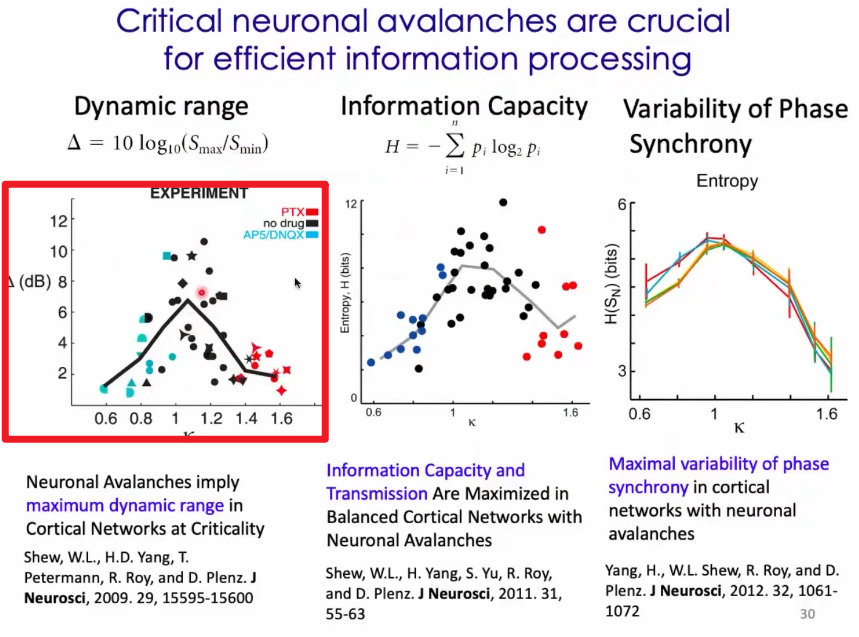
37、大脑有个特点,既需要同步,有需要随时解开这个同步。始终处于临界状态,能够随时切换为同步和非同步状态。这样能够对外界刺激随时做出响应; 这种状态的构建,需要花费很多的能量;
38、神经网络的震荡。神经元的发放率可以是很低的,但是震荡的频率可以很高。
39、震荡在神经网络中作用是:可以提供一种稳定的时钟,有一定的周期性;震荡还能辅助不同脑区之间进行信息的耦合和交换;回路可以作为一个振子,来运作;
40、神经科学的研究中,经常使用神经元发放率的变化来研究;
神经系统是一个功能复杂系统:
1、大脑神经系统在进化的过程中有很多进化压力,以及限制条件:比如能量、代谢、应用方面还要优化很多功能。
2、所以,生物神经系统中,有这种成本和效益的均衡; 这种均衡一定会反映到它的这种结构、网络连接、结构和活动的关系上边;
3、生物神经系统,到了今天这种程度,很大程度上是在低功耗限制下,无可奈何的组织方式。在没有功耗的约束下,人设计出来的系统,在某方面可以大大超越人的极限;
4、大脑中的能量都花费到哪了?第一,产生动作电位;第二,传输动作电位(神经递质的释放和重构);在这样的前提下,你必须得限制神经元发放的频率;同时,传输的路径越短越好;
5、大脑希望把能量消耗减下来,那么最有效的方案是从消耗能量最大的地方做起。
6、我们的大脑具有,低成本、高效能的特点:
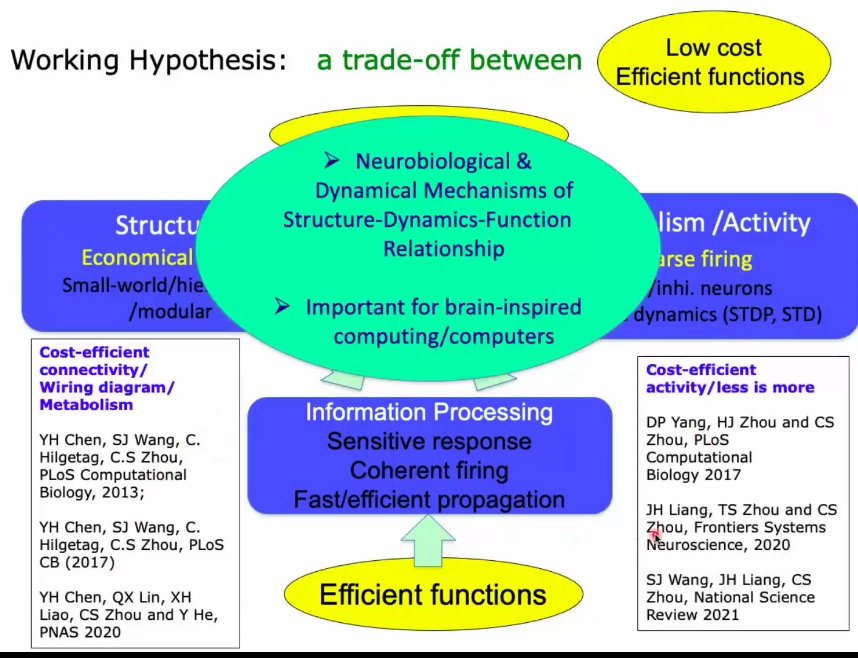
7、稀疏的神经元点火,怎么才能有效地组织起来进行高效的信息传递呢?
8、结构上经济的连接方法, 也得支撑起功能上最经济的动态活动;
9、神经元的发放是没有规则的。https://www.bilibili.com/video/BV1mu411y7M4?t=6657.6
神经动力学建模

1、通过模型,更好的理解看到的数据;
2、参数化的模型,和非参数话的模型;
3、自己设计一个模型,通过改变模型参数,能够迅速得到实验结果,在真实的实验中,往往不能轻易做到这一点。
4、如何描述系统的相互作用;
5、考虑数据和模型之间的融合;
6、模型是对真实系统的一个想象;
7、做模型研究中,需要考虑的四个问题:(1)计算和分析的复杂性要和机制理解之间取得某种平衡;(2)面对生物的真实性,有没有数据能够帮忙进行建模,即参数预测;(3)生物学家觉得很多细节都是很重要的,但是系统科学家,知道有主要影响因素和次要影响因素;(4)原则和细节如何达到某种平衡;如何把复杂系统的理解和神经科学家们的理解联系起来?
8、有两种建模方法:(1)现象级的模型;(2)机制性的模型;
9、第三种建模方式:介于现象性和机制性之间的模型:通过机器学习的方法,训练网络是的大致满足响应的功能,然后加入生物学中的一些限制,比如兴奋性神经元和抑制性神经元达到什么样的比例、等,这样模型在学习的过程中表现出来的动力学很有可能和生物的动力学类似;
10、神经生物学现有的模型:
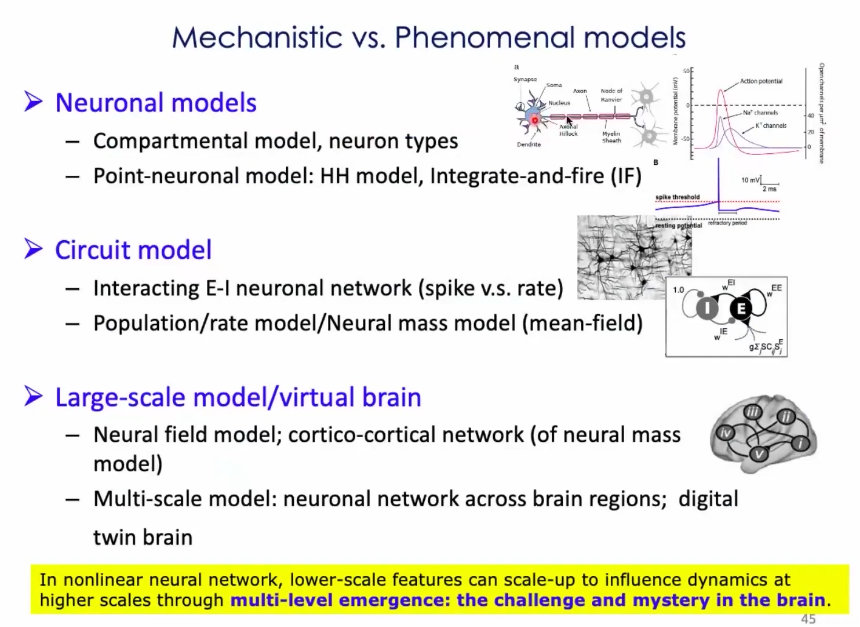
几个真实的神经动力学建模例子
1、思考的几个问题:(1)单个神经元无规则的发放怎么跟神经雪崩、震荡,联系起来?(2)什么样的成分起主要作用的呢?(3)什么样复杂的机制能够把动力学统一起来?(4)如何满足成本收益平衡的?cost-efficient;
2、周老师采用的分析方法:使用生物上合理的神经元网络模型,加上统计物理学上的分析;来理解这些特征。
3、 Random E-I Recurrent network的模型如下:(1)大概有2500颗神经元(80%的兴奋性神经元)、(2)随机网络、(3)连接概率约为0.2,泊松输入;
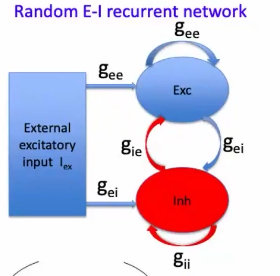
4、神经元的耦合,属于突触耦合:(1)一个神经元的激发会带给另外一个神经元类似alpha的输入;(2)兴奋神经元的窗口大小约为2~5ms,抑制性神经元窗的大小约为5~10ms;
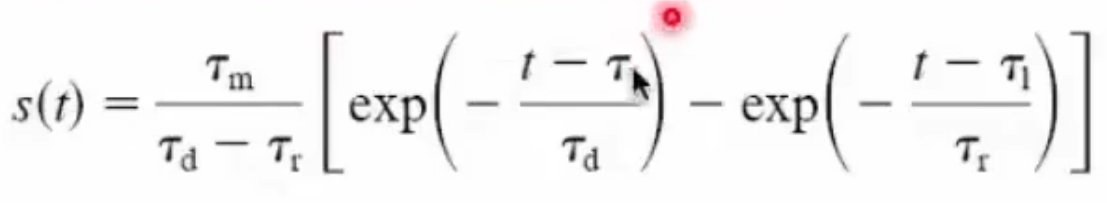
5、E-I模型的方程如下:对于一个神经元,首先(1)膜电位会有一个漏电,(2)兴奋性神经元输入给它的,有一个alpha的电导,电流依赖于现在神经元的电压(3)抑制性神经元输入给它的,(4)外界的输入;(5)电导的变化是两个alpha函数;兴奋的快一点,抑制的慢一点;
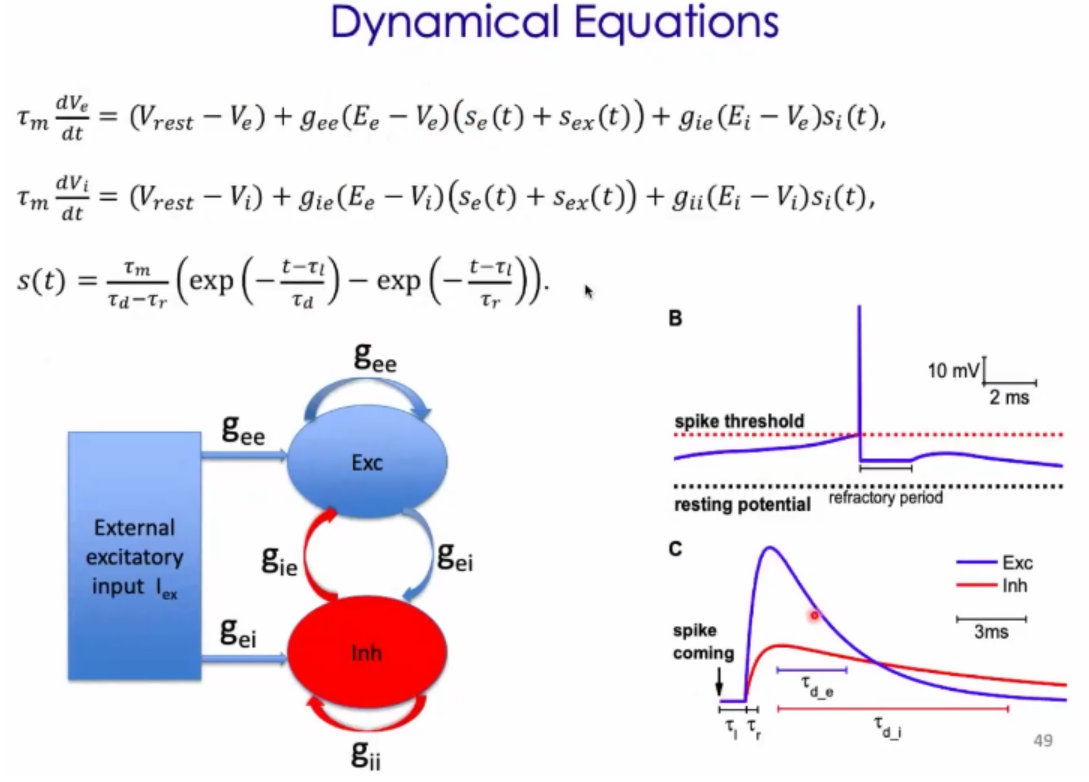
6、E-I模型是一个非常大的突破,还有一个介绍了gamma波的形成机制。之前人们认为:神经元的发放是无规则的进行,而且神经元之间没有关联性;后来人们意识到:神经元的发放可以出现同步,也可以出现震荡(但是震荡的时候不是每次都被激发);

7、周老师提出来的模型,统一了上述三者。(1)做到了兴奋性和抑制性的一种平衡;
8、周老师在自己的模型上,讨论了:(1)兴奋性神经元和抑制性神经元,窗口关闭的大小;当两者都比较大(6ms)的时候,出现的是Asynchronous状态(不同步的)、当激活t=4,抑制t=10的时候,会出现轻微的同步状态(moderately synchronized)、当激活t=2ms,抑制t=14ms时,会出现强同步状态(Strongly synchronized);
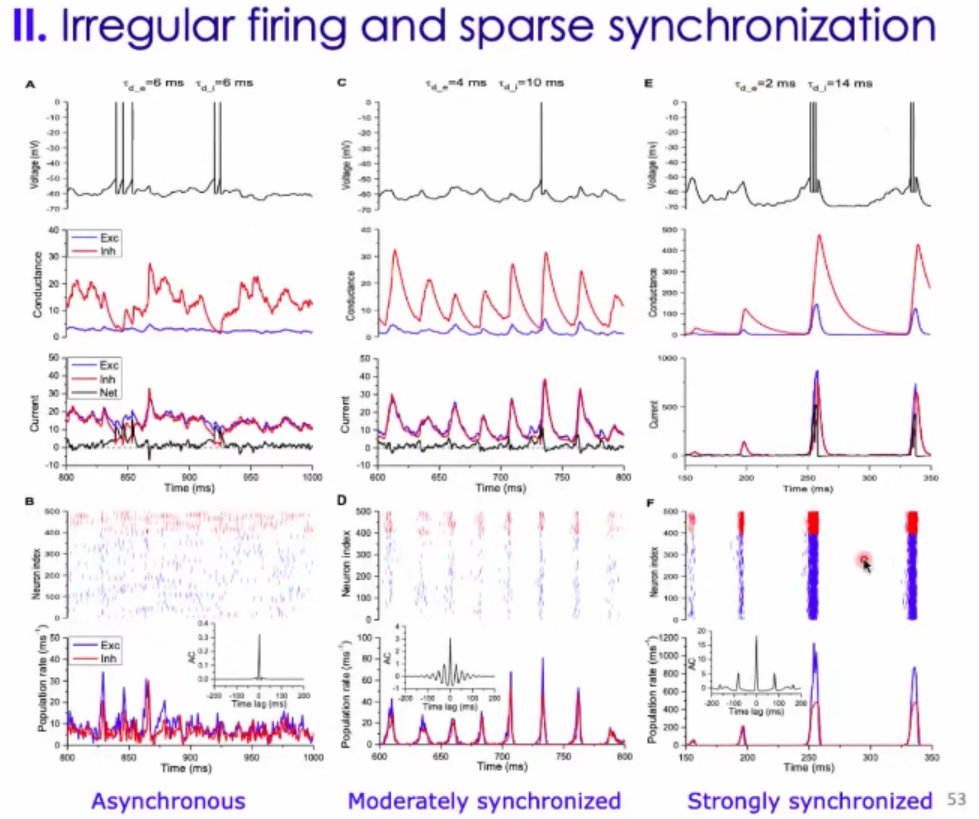
9、这个参数下(激活t比较小,抑制t比较大),神经动力学出现在临界状态,此时神经元的可以比较随机,也可以出现微弱的同步变化。
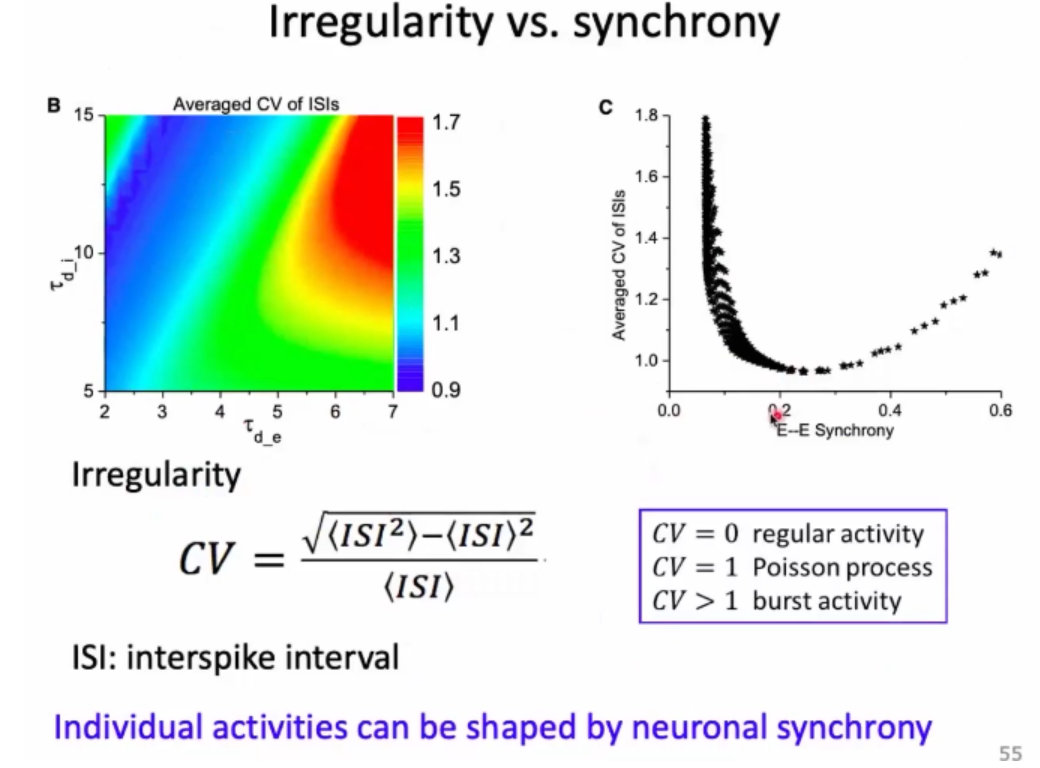
10、在过渡态,有比较好的幂率分布。如果是随机状态, 更像指数分布,
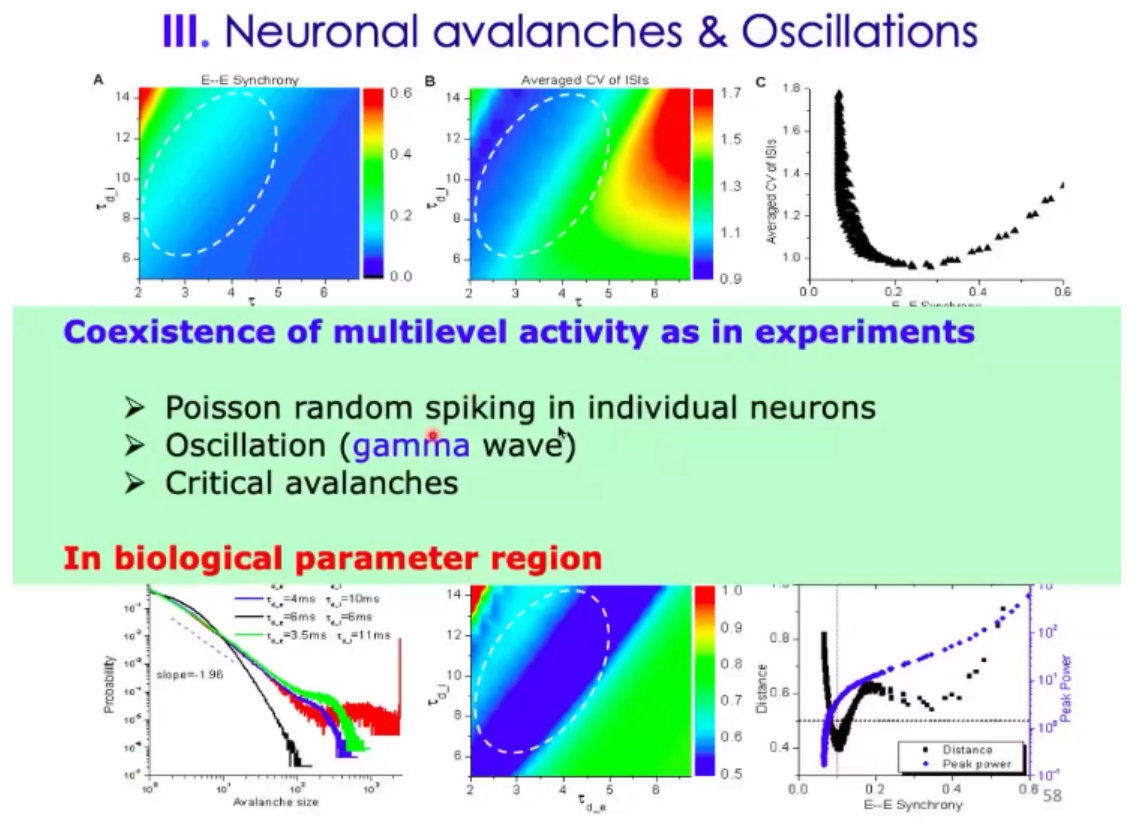
结论:神经元随机发放、震荡产生gamma波、以及出现雪崩是可以同时在这样的随机网络中出现的;
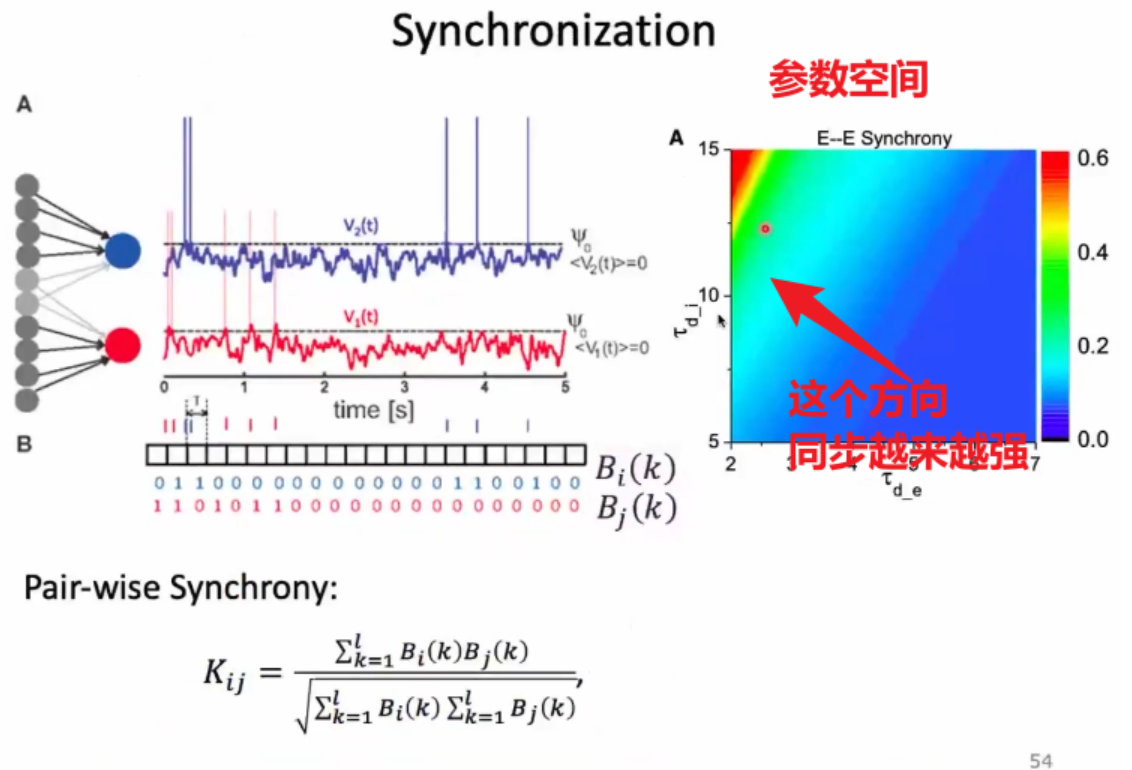
11、横轴是,神经元同步性的测量、纵轴是不规则性的测量、震荡的幅度、以及幂率的分布:
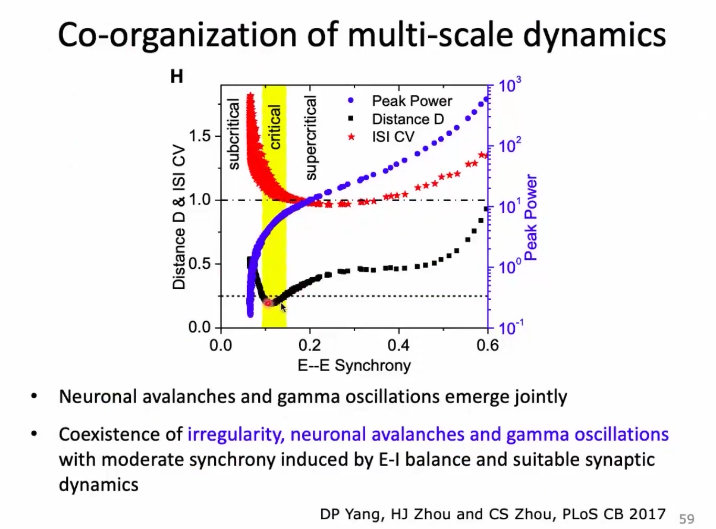
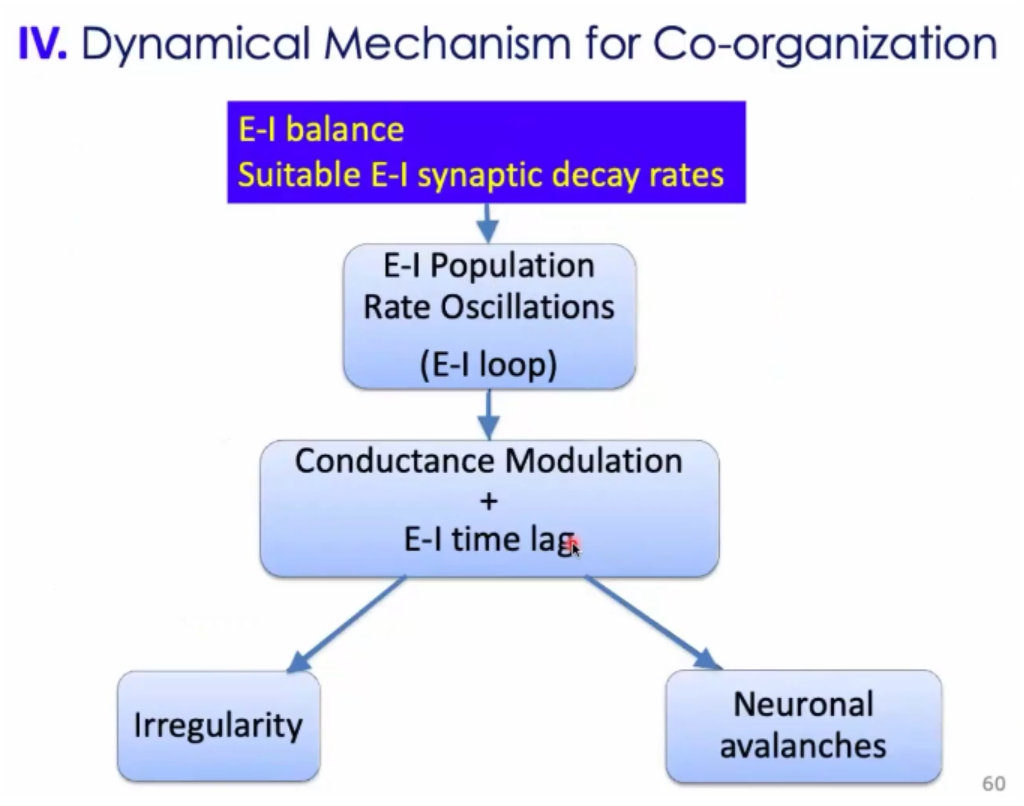
12、这种属于抑制平衡的状态;不是平均值上的平衡,而是静息上的平衡。兴奋和抑制有个loop。首先兴奋性神经元起来,导致抑制性神经元跟着起来,抑制神经元放过来会压住兴奋性神经元,但是两者的时间窗大小不一样,存在一个时间差lag,这个时间差lag的存在就允许神经元在外界的刺激下兴奋起来,进行发放;一旦发放了,下次回来的时候,就是一个随机网络,可能被压住了,表现出来的话就是其他神经元进行发放;宏观上,表现出来神经元的发放是没有规则的;但是在个窗口下,有很多神经元是有机会一起发放的;从而产生了雪崩;
13、一个非常形象的比喻:一个班级里边,小孩们吵吵闹闹的,老师呢是有一定容忍度的,说一两句也无所谓,但是超过这个容忍度呢,老师就会拿眼睛瞪一眼领头的学生,这个时候就安静下来了。过一会,又有其他学生起头吵吵闹闹,每次吵吵的学生都不是同一个学生。
14、理论上,如何描述这样的现象:可以简化成拥有6个变量的非线性方程;
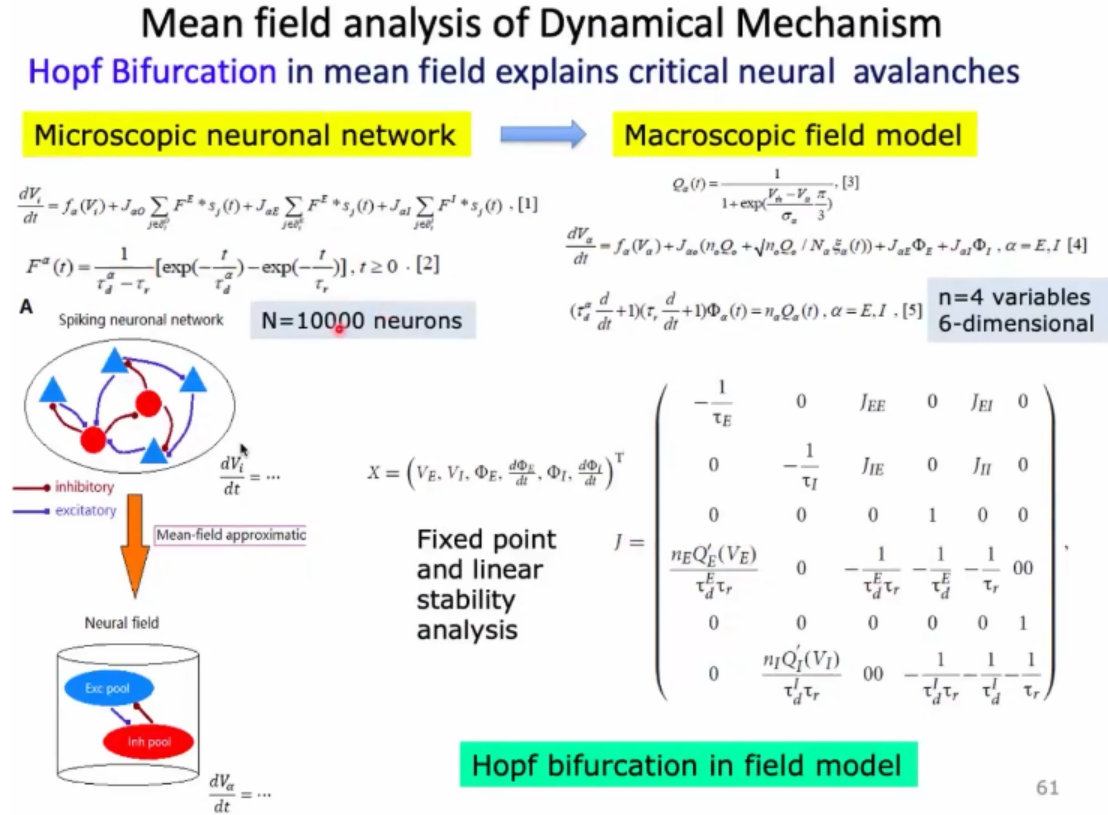
15、所谓模型中不同步的状态,就是对应到发放率是一个不动点的;平均来说它有一个固定的发放率;
16、有了这个模型后,就可以分析非线性动力学的不动点。有个稳定点,它是稳定的,或者不稳定的。然后给它一个局部的微扰,稳定不稳定呢就看它的特征值。如果特征值是正的,小小的扰动就会被放大,这个稳定点就站不住了,进入震荡的状态;从没有震荡到震荡这个状态的过渡中,可以测量震荡的这个频率和神经元发放的频率;
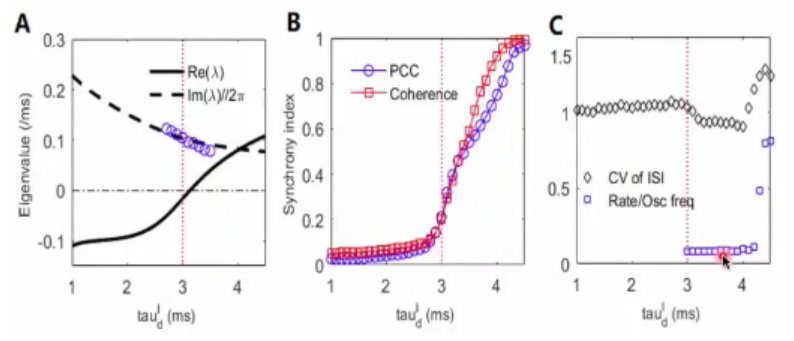
1/10的结果和生物上的测量保持了一致性;
17、在非线性动力学中呢,这种正好处于临界的状态,也叫做Hopf分叉。即从没有震荡到进入震荡的过程;
18、雪崩也可以进行刻画,比如抛落、大小。这些和幂率指数之间的关联;
少即是多:神经回路动力学的成本效益
1、神经发放的经济学;神经元的发放可以表征一些信息;希望表征的容量尽可能的大;
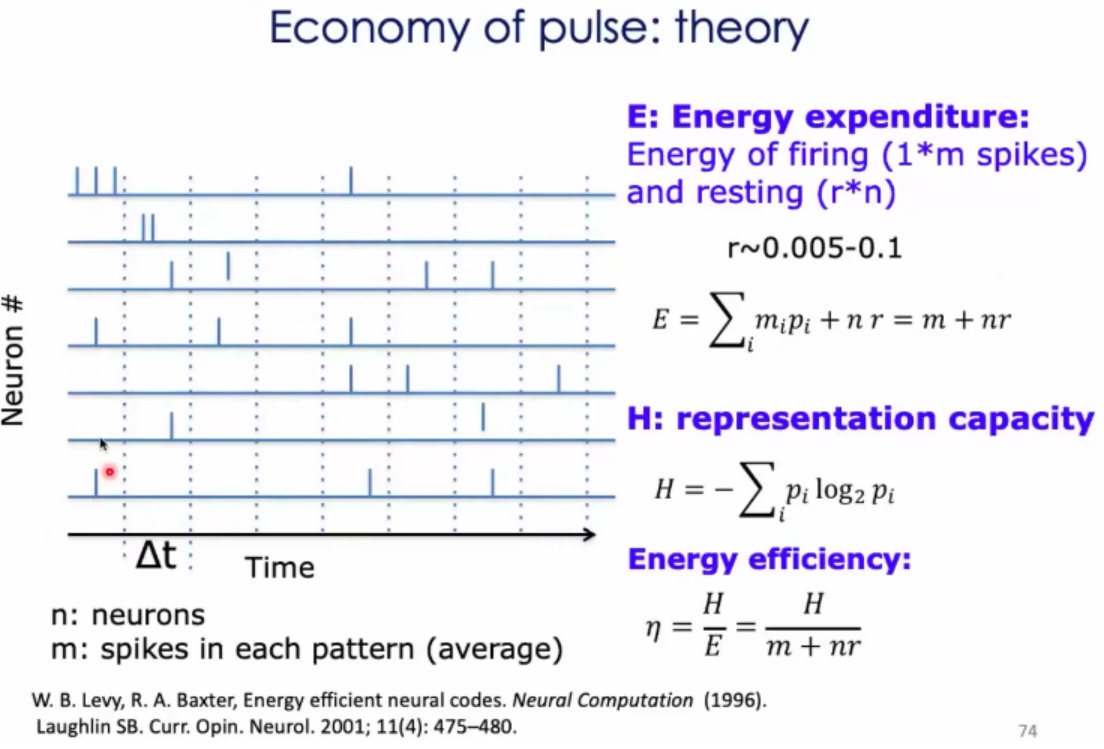
2、构造一个熵最大的模型:
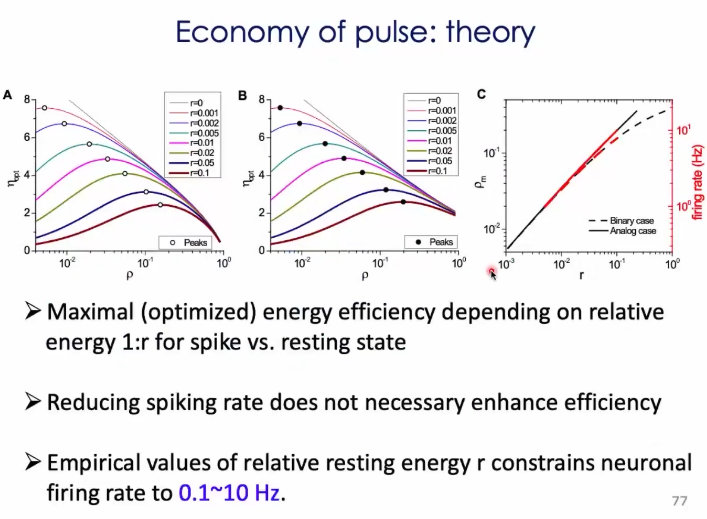
3、在参数空间中,把神经元的发放率和能量效率给画出来。
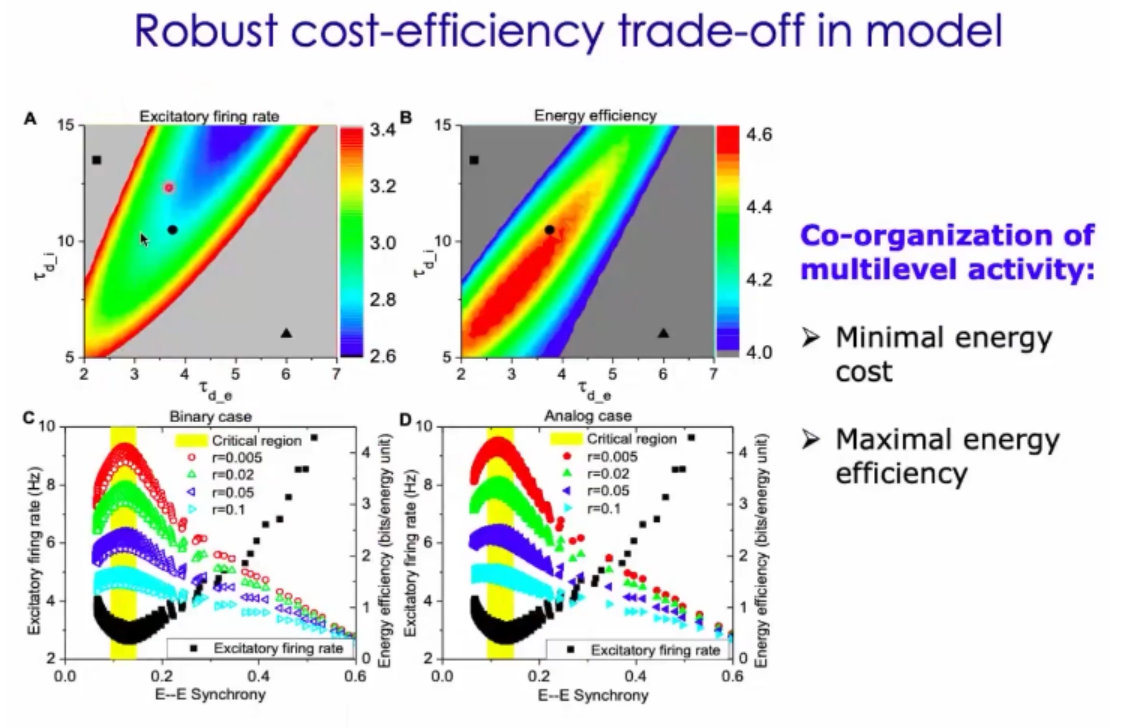
结论:在临界状态下,发放的代价是效率是最高的,代价是最低的;
4、上述的探究都是在局部的随机网络中进行的,实际上网络是存在结构和层次的。
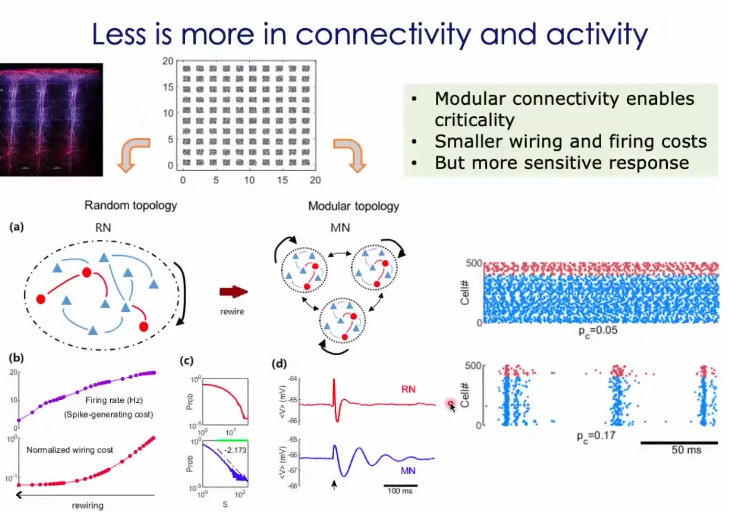
5、为什么紧密的连接,会产生关联的活动呢?因为,当两个神经元有共同的邻居后,他们的输入就被关联起来了;
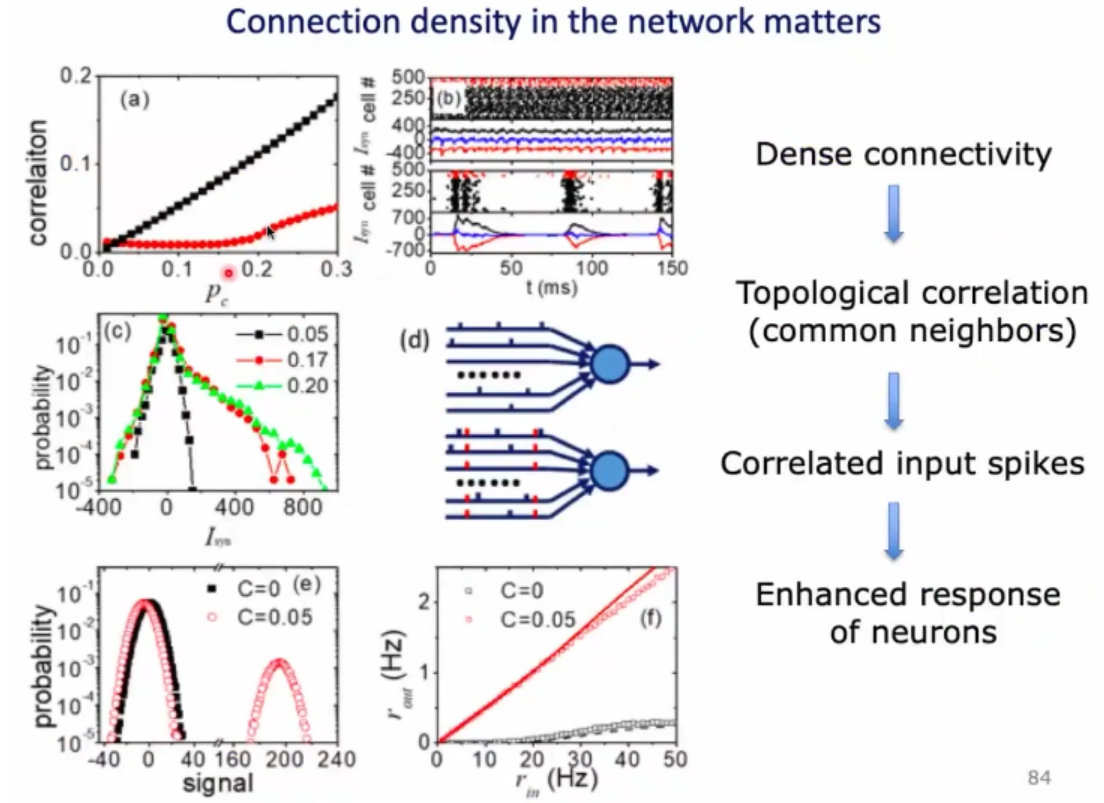
6、总结:(1)神经动力学是多尺度的,很复杂;(2)一方面收到能量的限制,另一方需要满足有效的信息处理;(3)周老师构建出来的是这种兴奋抑制平衡的神经网络;这种网络会出现集群和震荡的发放;(4)兴奋和抑制的loop,导致时间窗的随机,在动力学上,就会产生自反馈。有延迟的抑制自反馈呢,在理论上就会产生 hopf分叉;从不动点,到震荡的相变;这属于大自然的设计。(5)这种组织方式可以花费很少的代价,实现很高效的功能。
信息处理中的复杂神经动力学-学习和记忆补救
1、大脑的自发活动和刺激之间如何进行交互?(1)减少trail-to-trail的变异性;(2)偏离临界性,很快又重构这种临界性;雪崩服从幂率分布(3)改变震荡的频率;

2、共识:什么是记忆?目前的共识是,大脑中有一群神经元可以一起激发来表征记忆。
3、几毫秒的时间尺度,对于记忆的形成和突触的变化也是非常重要的;神经的可塑性也是一个非常重要的点(Plasticity)
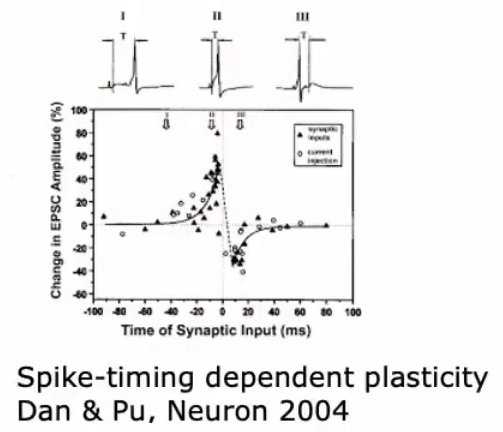
4、 一旦出现gamma波(或者说gamma波涌现出来),神经系统的学习率也得到了迅速的增强。
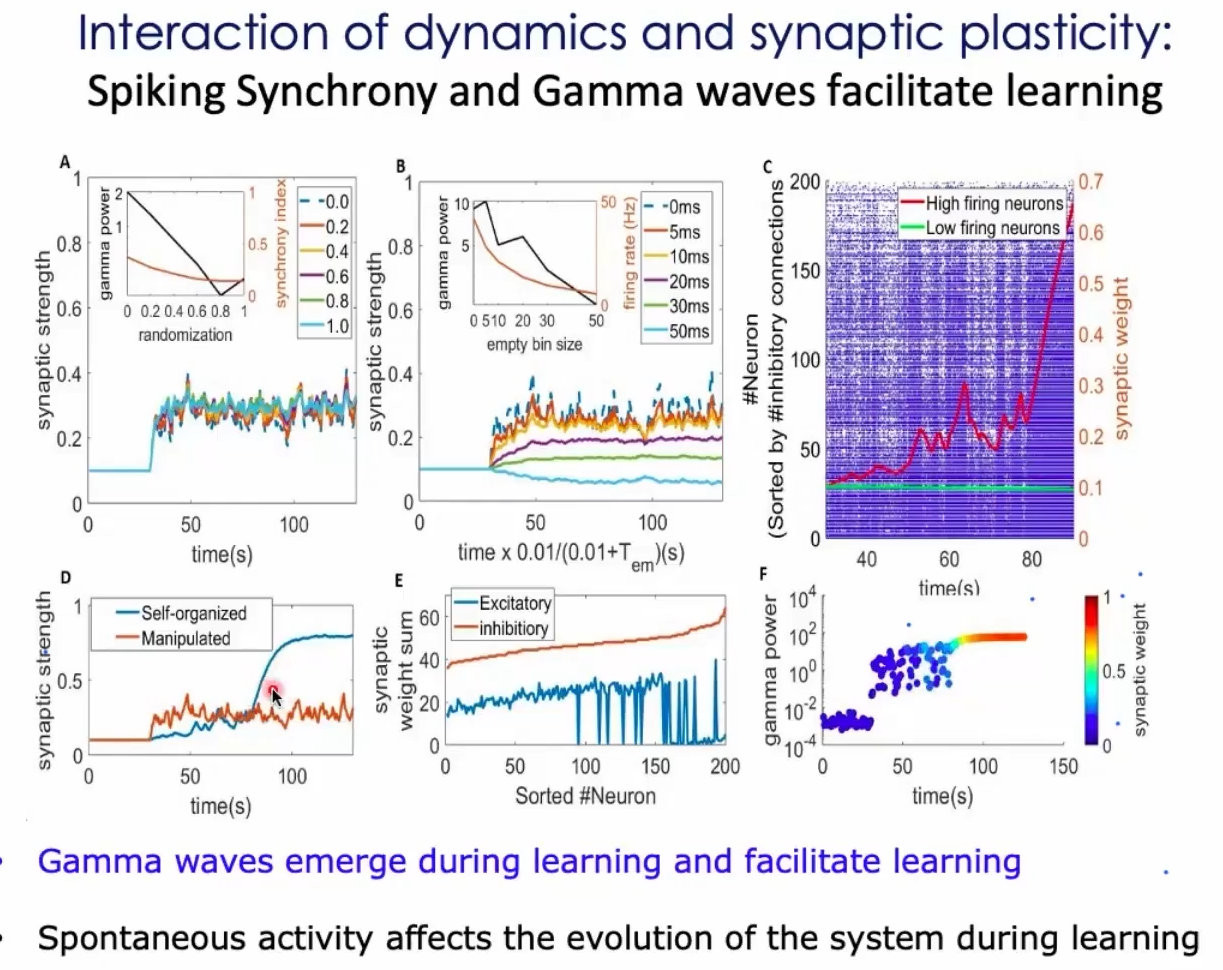
在意识恢复过程中复杂的皮层波的传播
1、进入更大的尺度,皮层波;
2、悉尼大学的Gong老师,做计算神经科学非常厉害的一位老师;使用了Phase velocity field(相速度场)
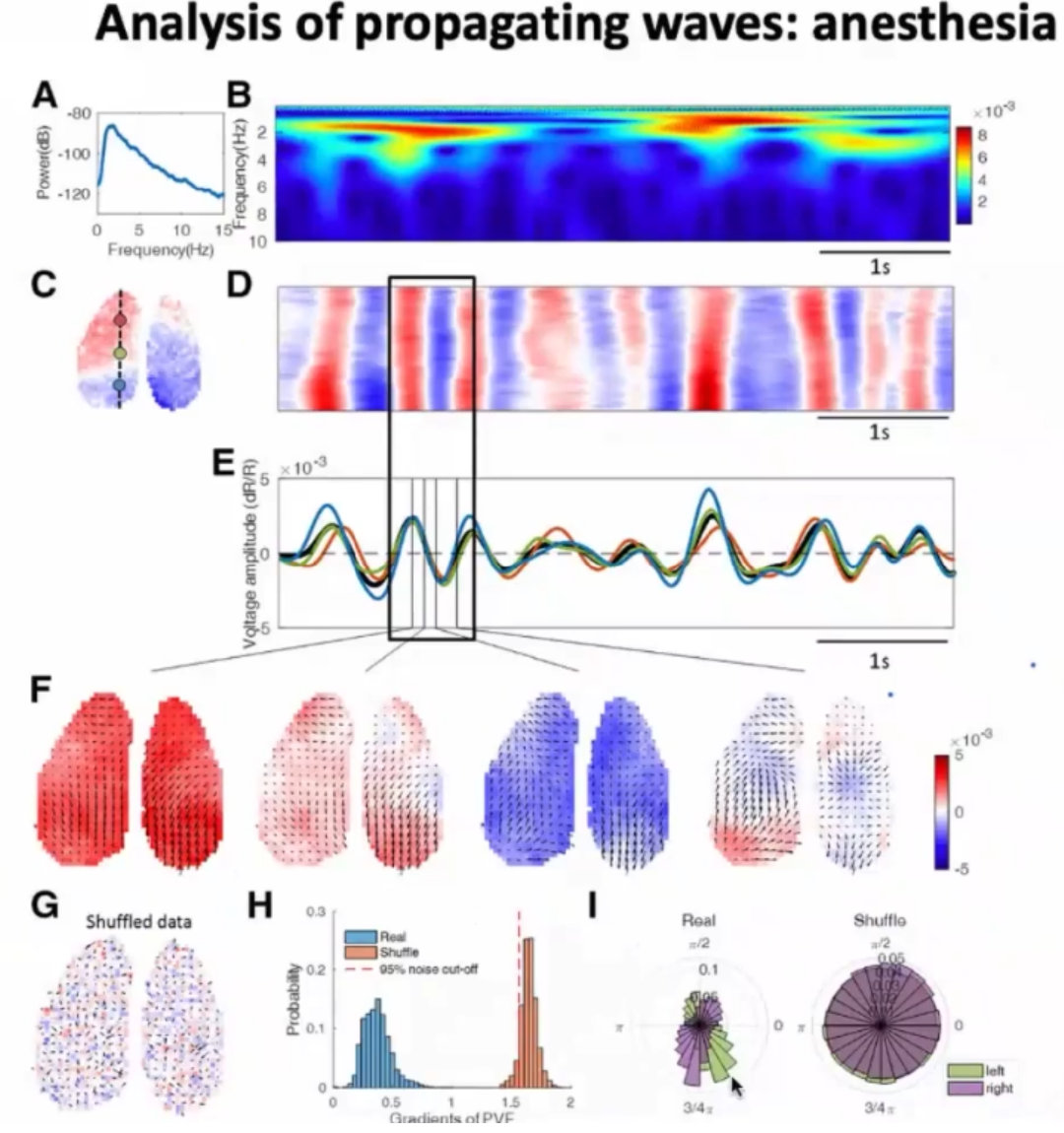
3、接下来就可以对波源、波汇、鞍点进行分析;
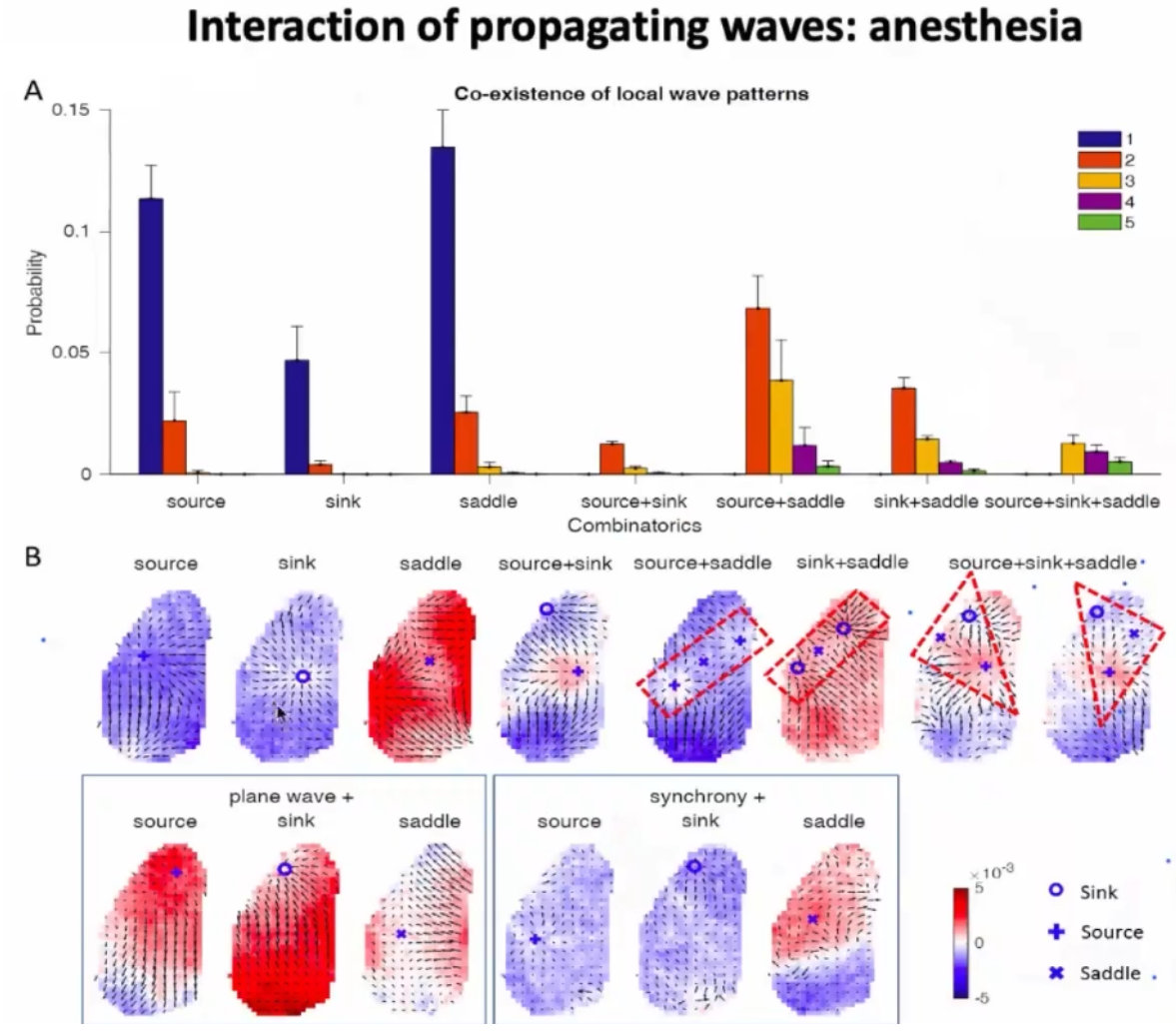
4、波源分布的结构和解剖的结构也是有联系的;
5、从麻醉到清醒的过程,也是一个意识恢复的过程;
大规模功能连接:层级模块化组织、多样性、平衡性和认知能力
1、模块化、层次化支持神经网络的功能分离。
2、结构和模块的功能影响;
3、Hyper-community(不要用Rich-club)
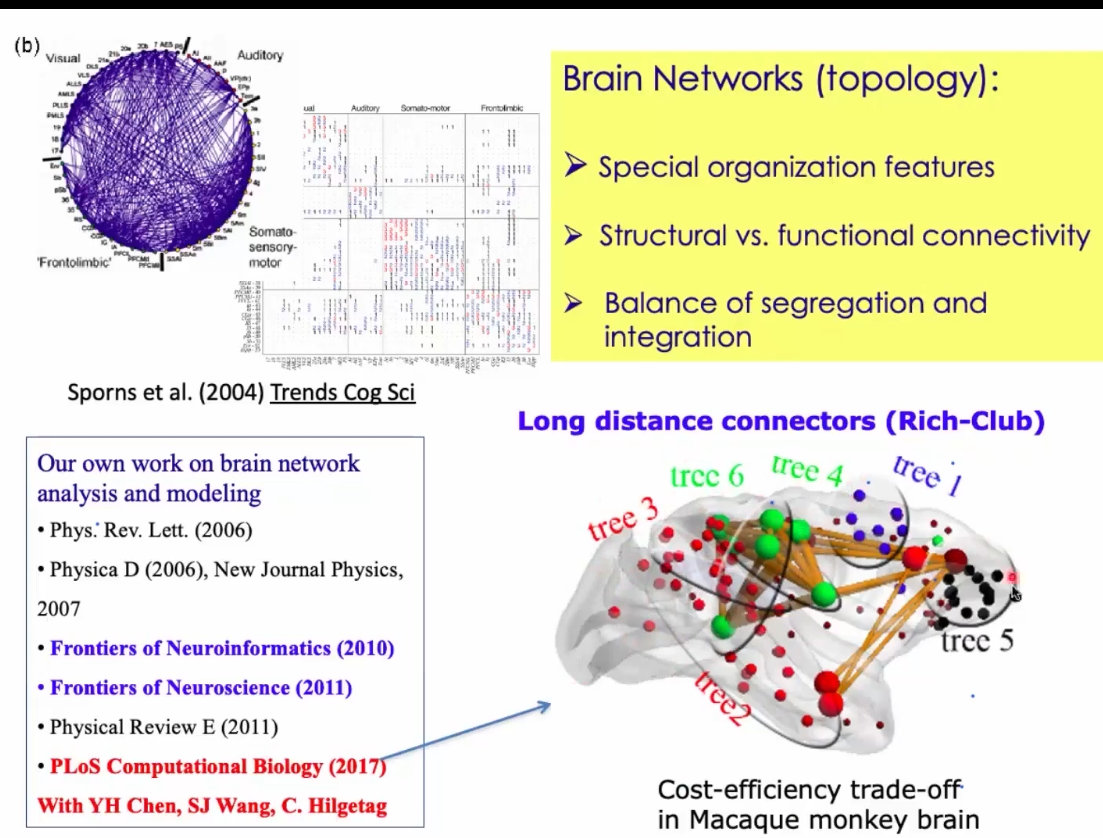
4、看似很复杂的一个模式,进行本征分解之后,会得到两个非常简单的模式的叠加:
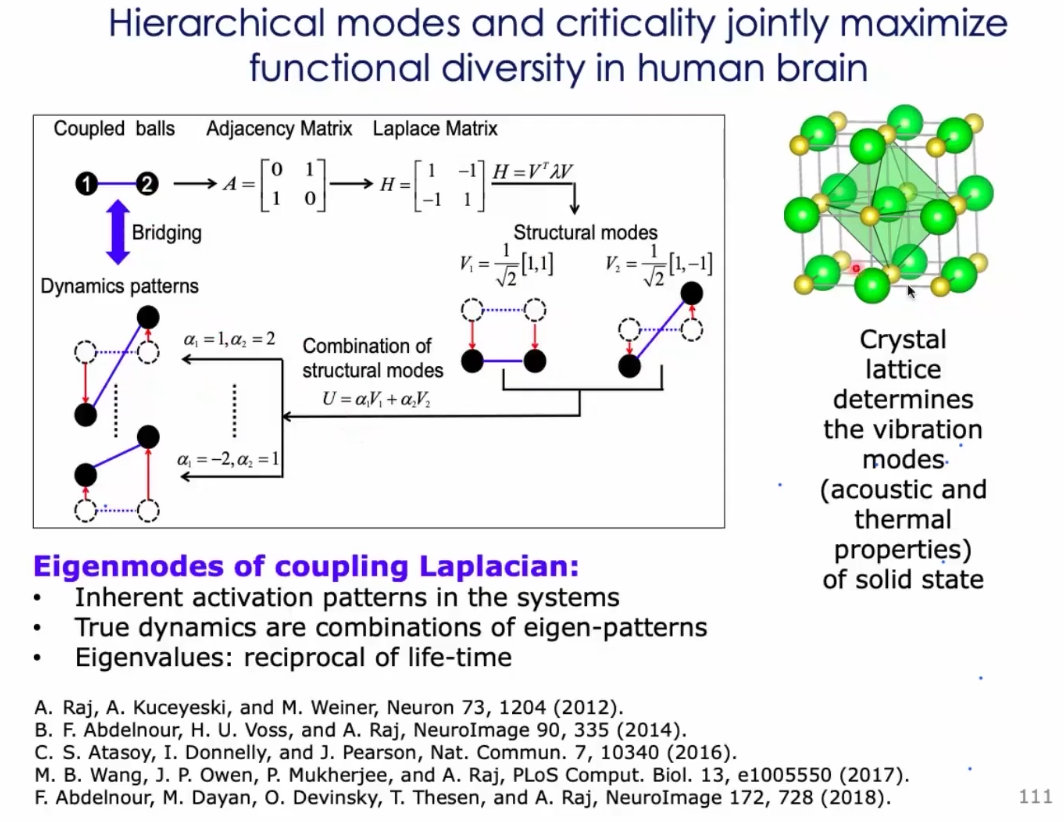
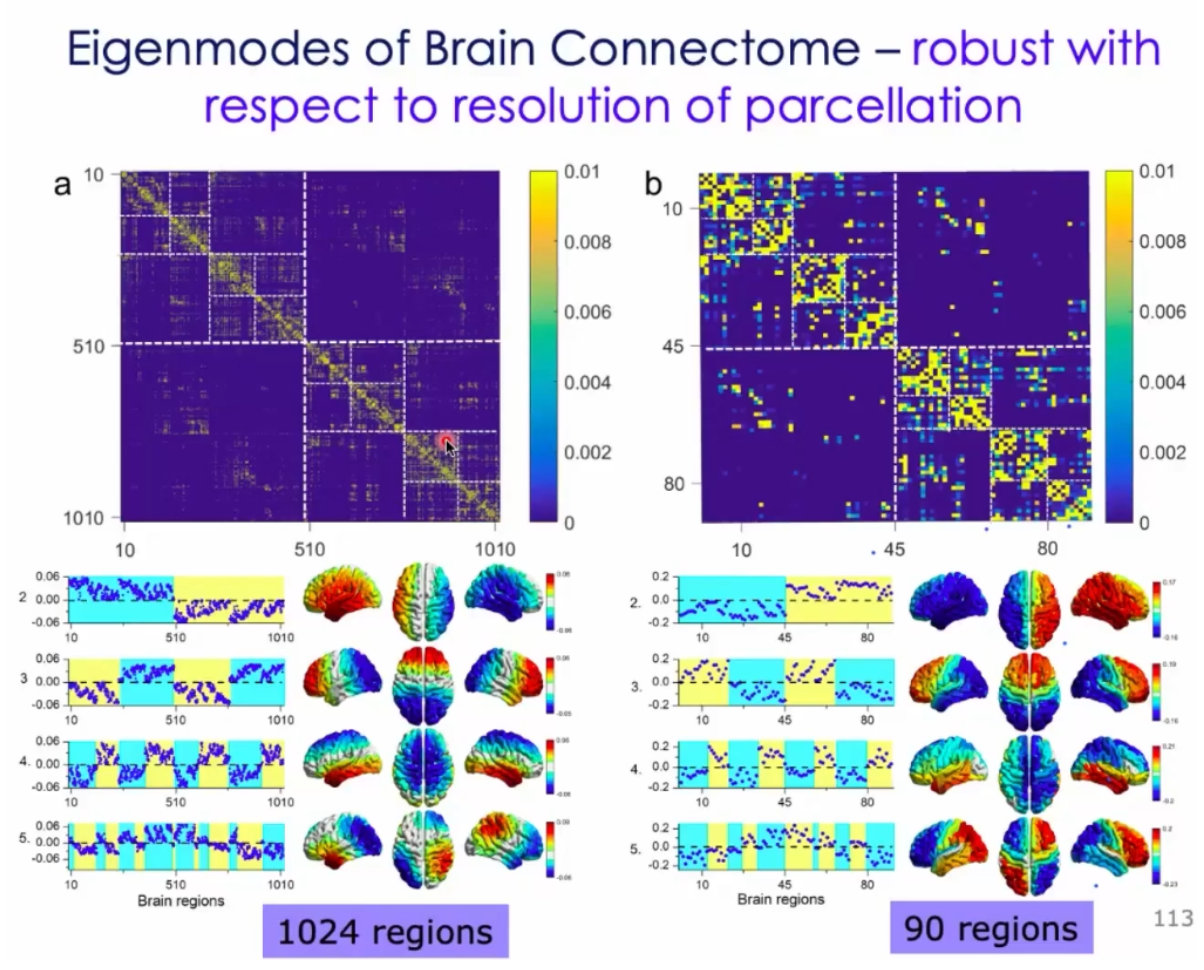
5、大脑中存在很多模块化的机构。通过拉普拉斯分解,就能得到这样的结构;
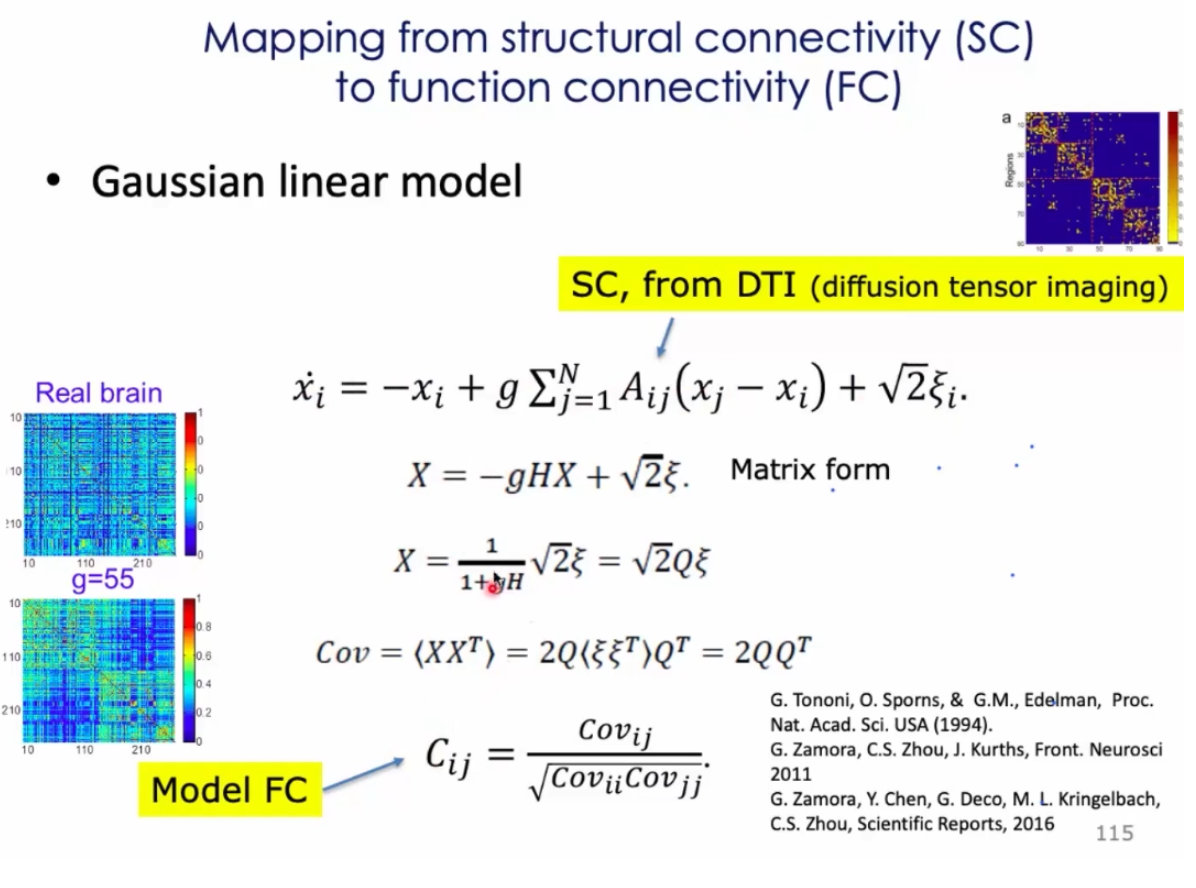
6、直接把结构翻译成功能连接:
7、用雪崩来测量人的大脑:
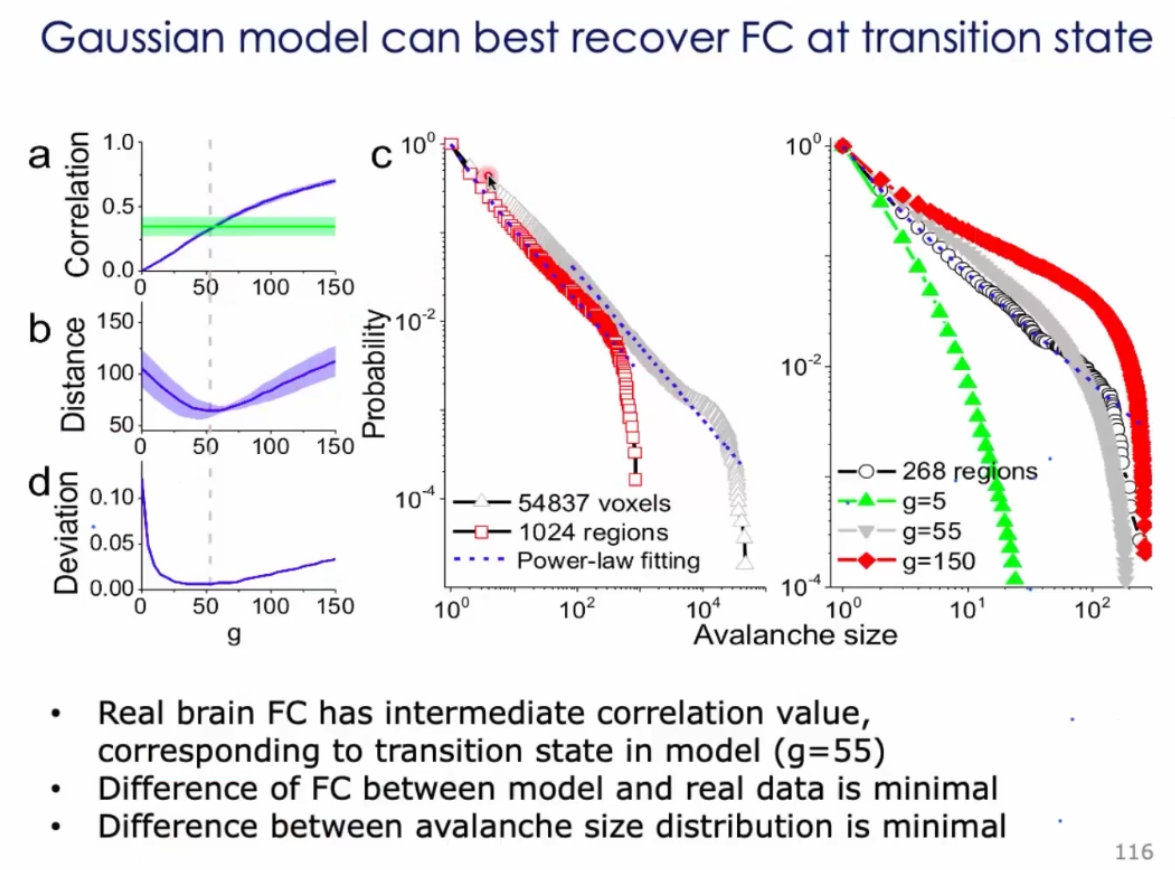
8、如果大脑脑区和脑区之间的连接过于强的话,就类似与癫痫状态,无法分化出具体的功能:
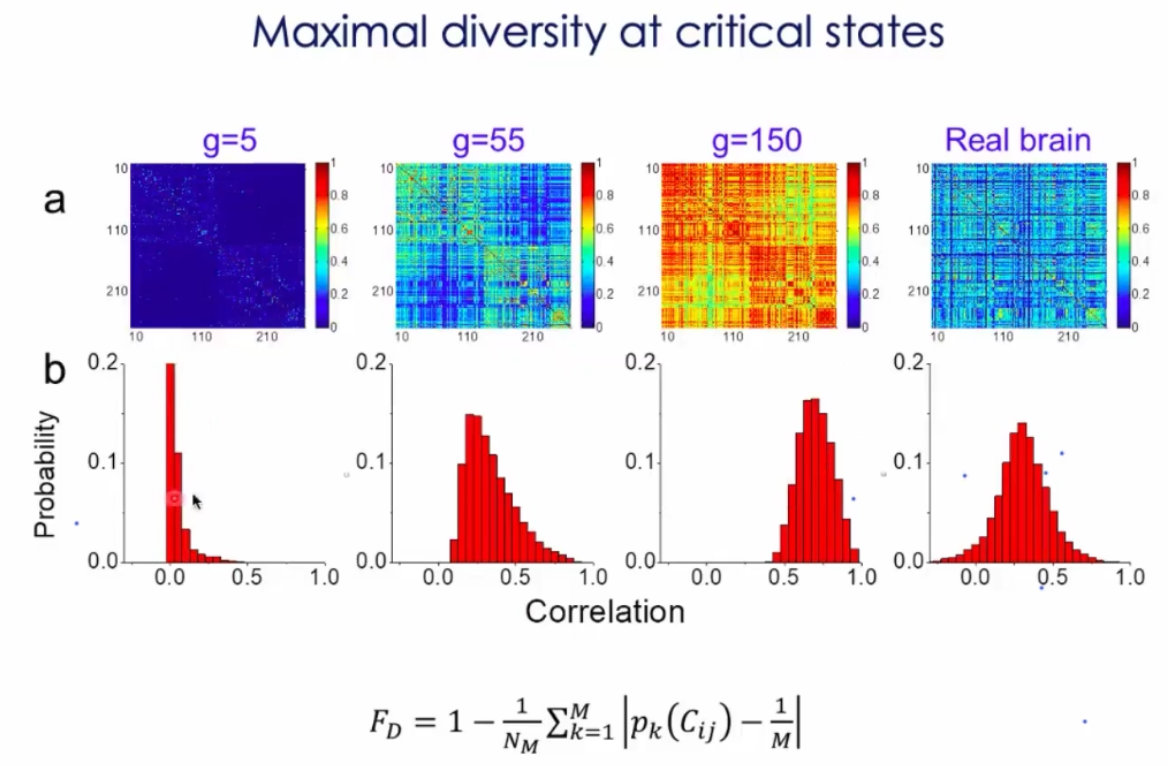
9、这种分析思路非常值得借鉴,我不直接给一个硬阈值,这样会把有意义的连接直接绊掉。而是设计了一个模型,通过遍历模型的参数,看看什么参数下,模型的结果和真实结果最接近,然后理解数据背后的意义;
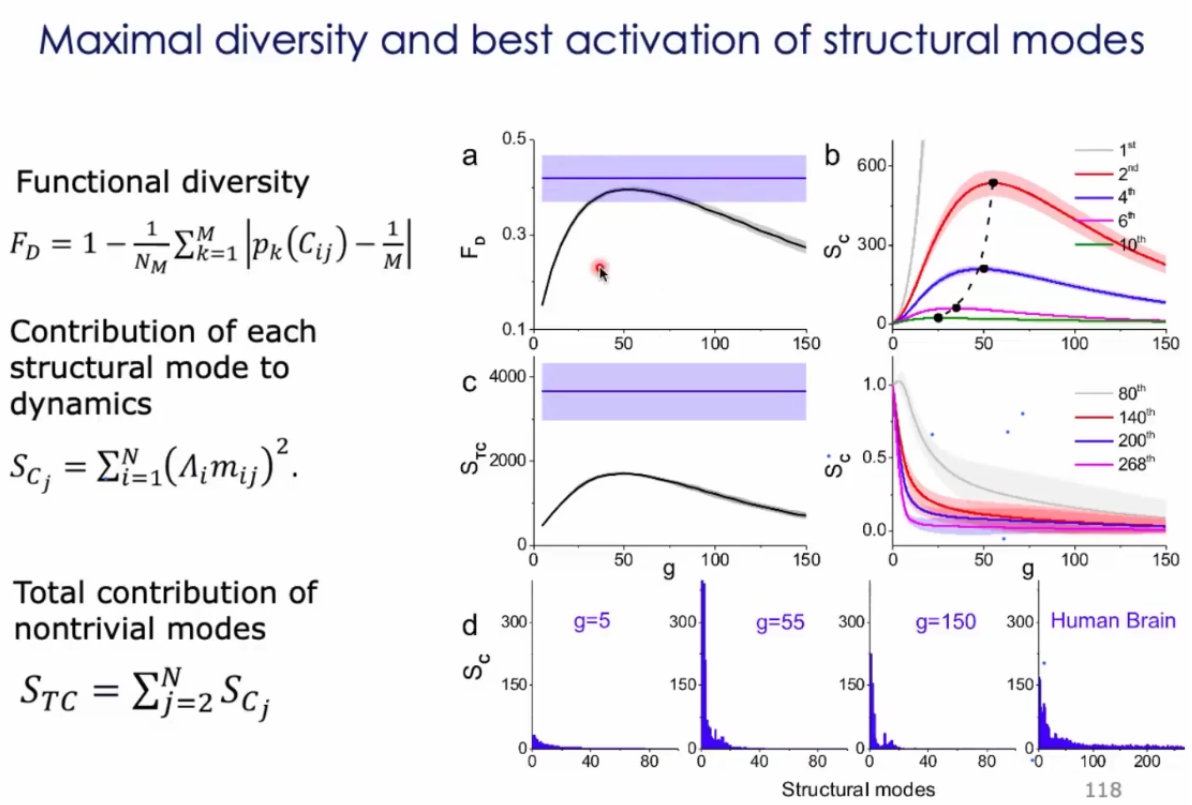
10、通过模的测度,定义了一种所谓功能的整合;
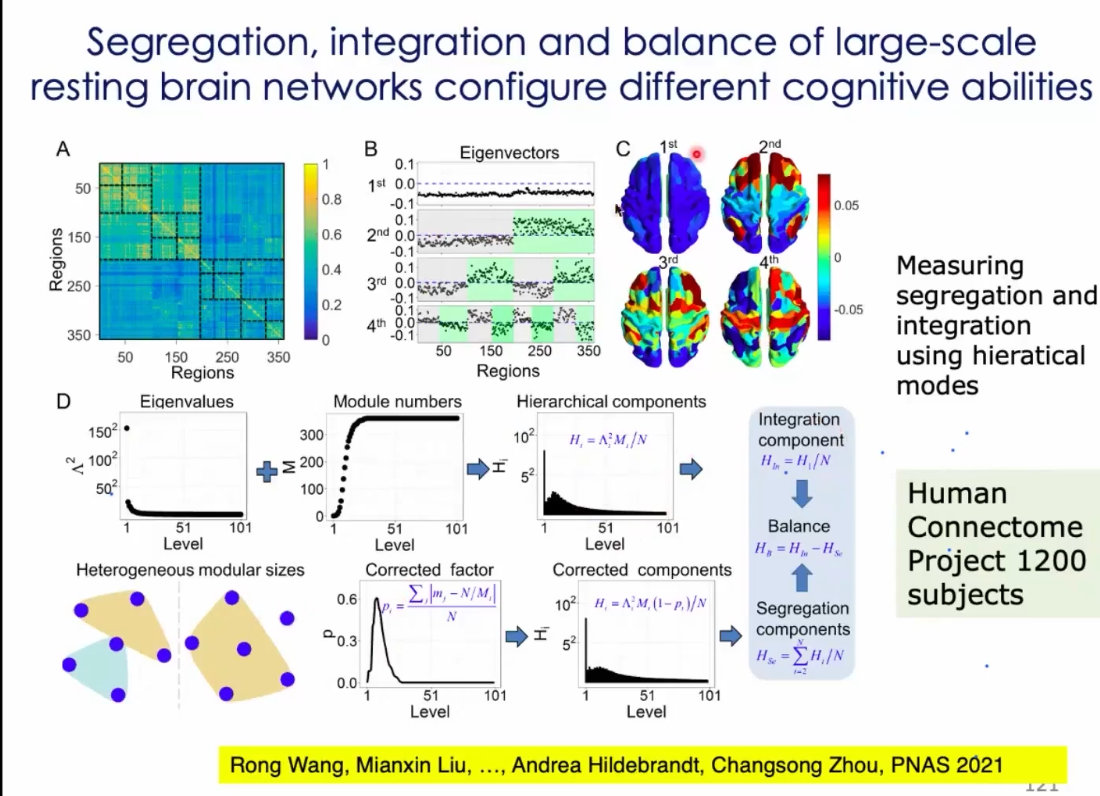
11、个体的差异,能够来表征我们的能力、疾病等…

机器学习的神经计算模型
1、人工智能和神经科学结合的一个方向(周老师的思考)
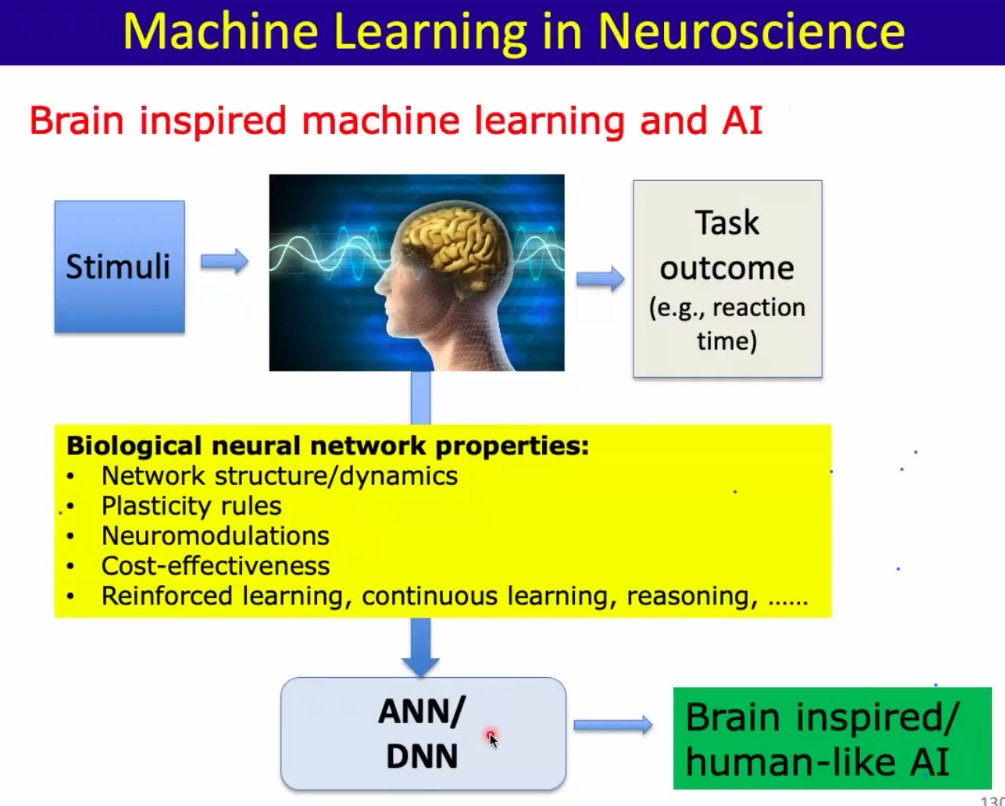
2、如何感知时间,维护时间?

总结 Summary
1、大脑是一个复杂动态网络系统 ,结构连接的活动、行为、障碍。都是有可能通过复杂网络连接的框架,进行些分析的;基本的想法是:模型和动力学的建模,可以帮助我们理解大脑的工作原理,这种相互作用,或者跨层次的原理。这种理解,可以指导我们理解和分析这种多尺度的数据;没有系统的认识的话,去理解大脑神经元的工作或许是很辛苦的;
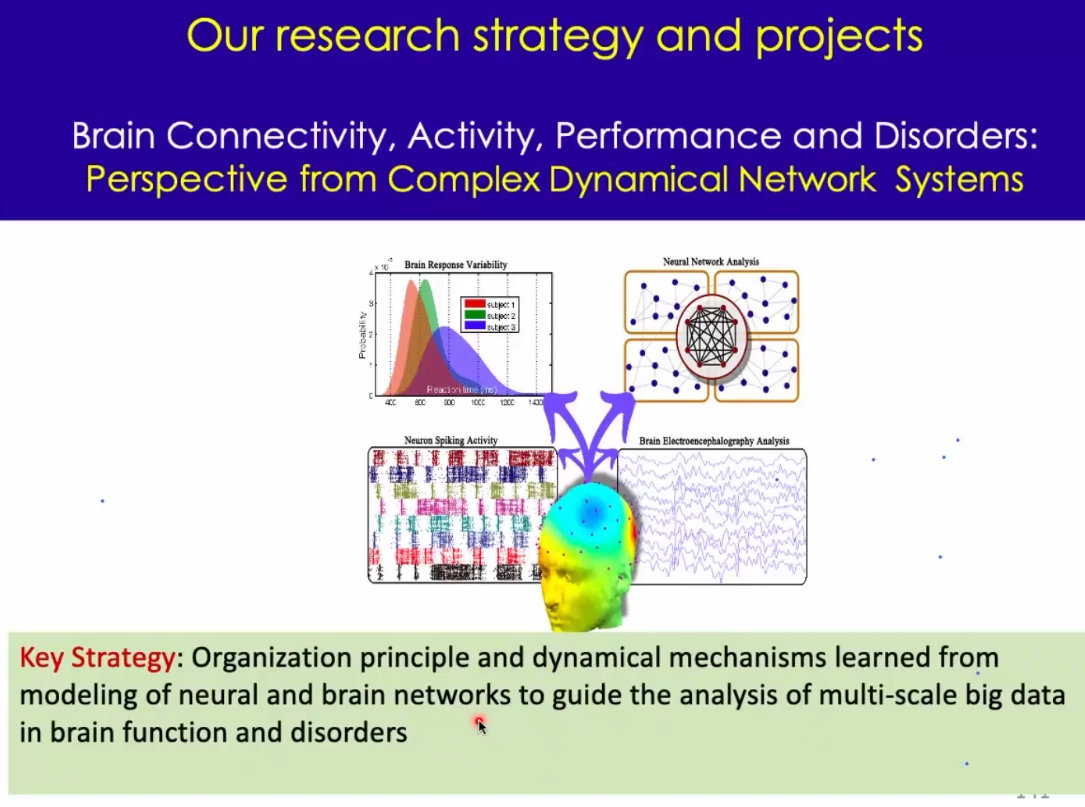
2、从复杂网络、动力学的视角理解神经网络:一些现成的工作;(1)多层次、(2)临界性、(3)功能分离、(4)个体差异、(5)cost-efficiency

3、实验室的基本框架:
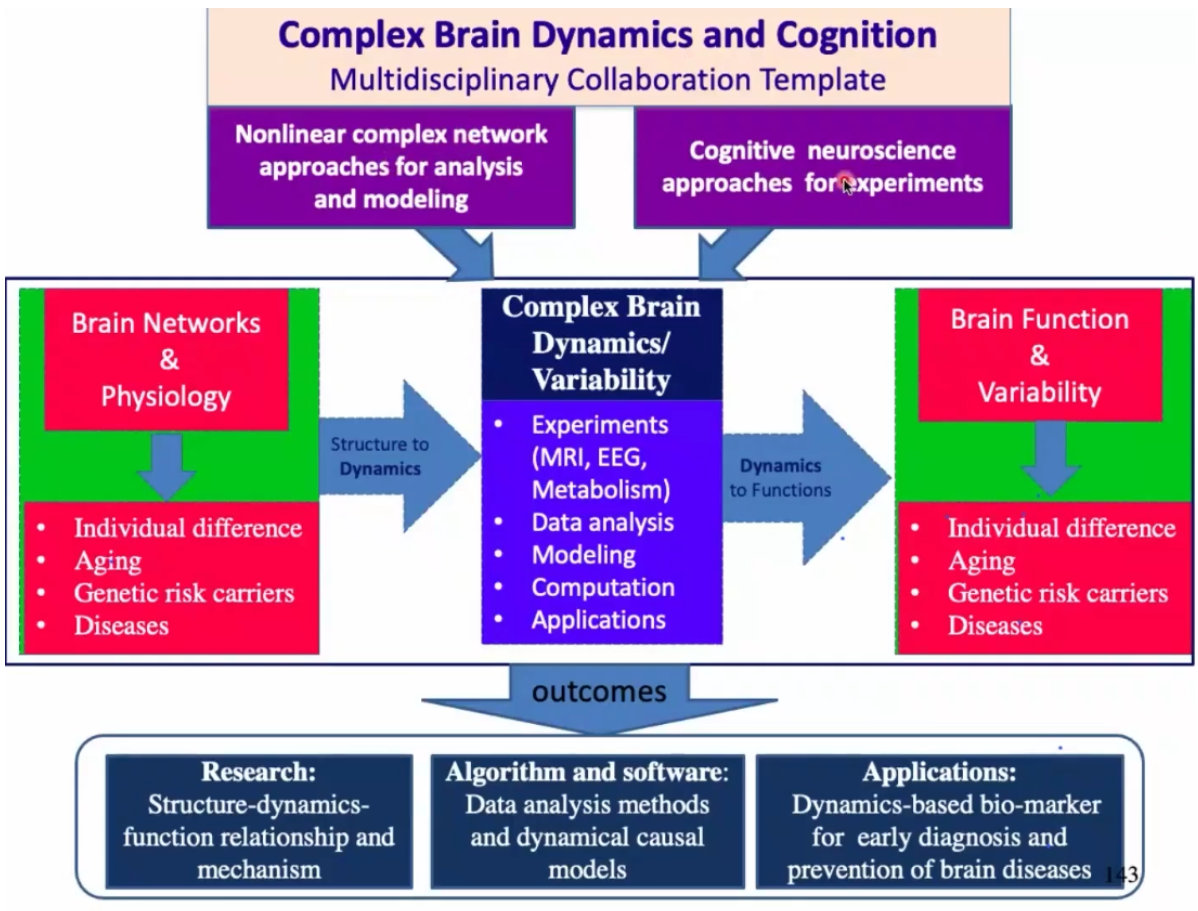
4、脑神经科学的展望:复杂中也有可能包含很多信息。

5、大脑又复杂又高效,如何平衡的?
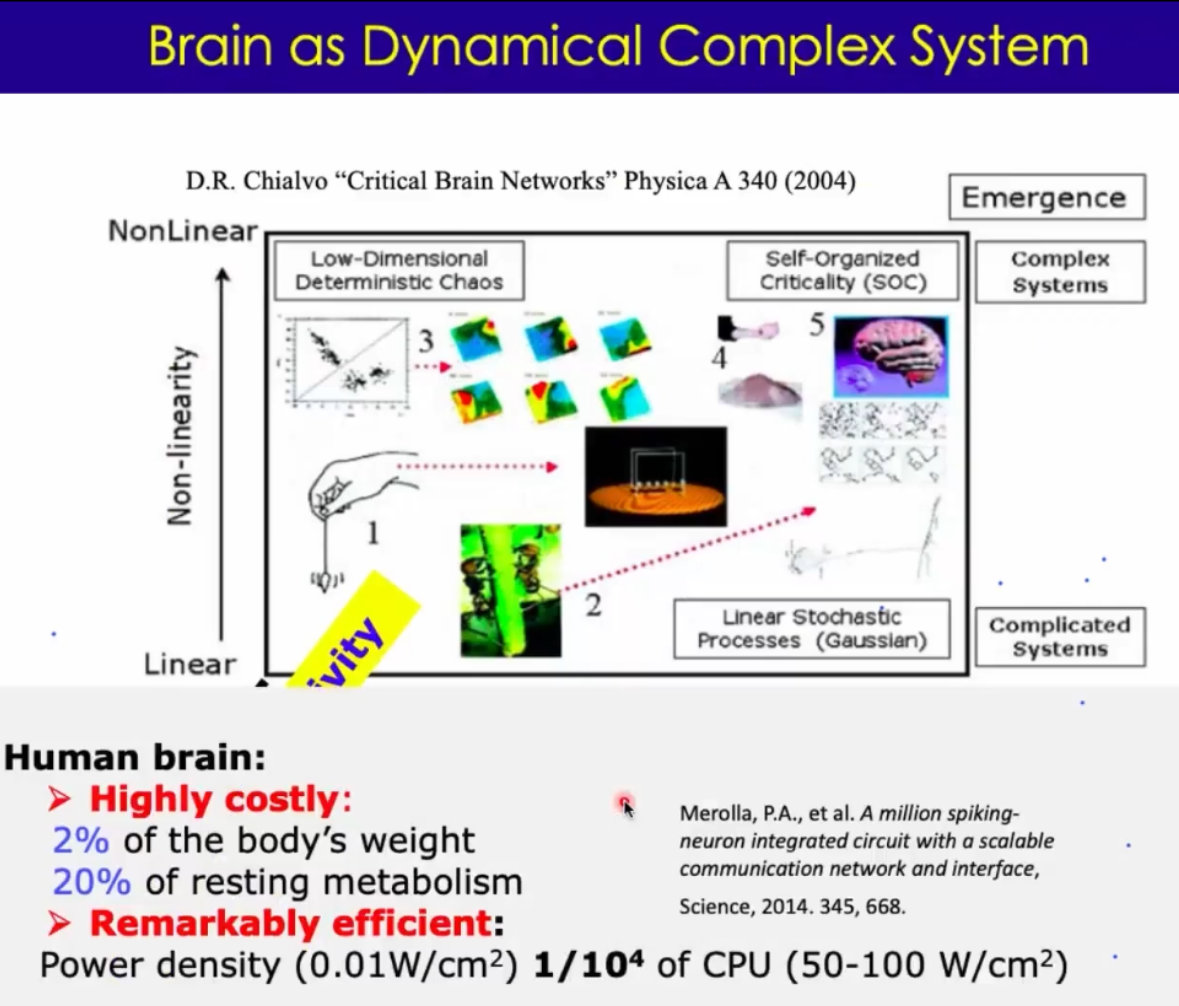
6、动力学、系统的方法;