名词解释-March
Backprojection
The backprojection is calculated from the histogram. It basically replace every pixel by it’s probability to occur in the image. It is not really useful to use it by hand, but this is used by other algorithm like meanshift. The example below shows the common usage of backprojection associated with Region Of Interest. In this example we select a rectangle in the upper left corner of the image, we compute the histogram and then apply a backprojection on the whole image to detect others parts of the image which have the same histogram.
“replace every pixel by it’s probability to occur in the image”——把每一个像素点替换成它所出现的概率
http://www.robindavid.fr/opencv-tutorial/chapter4-histogram-and-backprojection.html
understand the backprojection in an other way
https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_imgproc/py_histograms/py_histogram_backprojection/py_histogram_backprojection.html
介绍CAMshift之前,我必须得先介绍一下MeanShift。因为CAMshift的全称是Continuously Adaptive Meanshift,其中就包含了MeanShift。
Meanshift
直观地看,Meanshift非常容易理解。假设你有一堆点,然后给你一个小窗,你需要做的是通过移动这个小窗,使得窗里的点数尽可能得多。如下图所示:

初始给定一个蓝色圈圈,叫C1,其中心用蓝色方框表示,叫C1_o。那么,你计算一下蓝色圆圈的重心,你会得到C1_r(由一个小蓝圈表示),它是这个蓝色圈圈的实际重心。很显然,两者并不一样。接下来,你需要移动你的圈圈,使两者重合。然后计算新圈圈的质心,大概率的,新的质心和中心还不重合。那么,你就再移动你的圈圈,重复这个过程,直到两者基本重合(或小于给定的误差)。最终,你会得到一个包含最多点的圈圈,在图中被标记为绿色,命名为C2。
这个过程可以由以下的GIF动画,形象地展示出来:
https://docs.opencv.org/master/meanshift_face.gif
通常情况下,我们是在histogram backprojection image上做的。当目标发生运动时,在histogram backprojection image很容易看到。那么,meanshift通过移动窗口就能定位到目标的新位置上。
下图是用meanshift追踪一辆汽车的结果:
Camshift
如果你仔细观察这个结果,很容易发现问题:我们的窗口大小是固定的,不管汽车离我们远,还是离我们近。这显然是不够好,我们需要让我们的窗口自适应:不仅仅是大小,还有方向。这个解决方案来自OpenCV Labs,并叫做CAMShift(Continuously Adaptive Meanshift)。文章的作者是Gary Bradsky,发表在1998年。
首先他用的是meanshift,一旦meanshift收敛了,他就更新窗口的大小,$s = 2 \sqrt{\frac{M_{00}}{256}}$。同时还进行椭圆拟合得到最佳的方向。在新的scale下,再应用meanshift,如此迭代直到达到一定的准确率。
结果如下所示:

这个过程可以由以下的GIF动画,形象地展示出来:
https://docs.opencv.org/master/camshift_face.gif
投影变换
投影变换(projection transformation)是将一种地图投影点的坐标变换为另一种地图投影点的坐标的过程。
根据投影中心与投影面之间的距离不同,投影可分为平行投影和透视投影。投影中心到投影面的距离为无限大时得到的投影称为平行投影,而对于透视投影,这个距离是有限的。平行投影又可分为斜投影和正交投影。投影方向不垂直与投影面的平行投影称为斜投影,投影方向垂直于投影面的平行投影称为正交投影。正交投影的最大特点是无论物体距离视点(眼睛或相机)多远,投影后的物体尺寸保持不变,常用于绘制物体的三视图。

刚性变换
只有物体的位置(平移变换)和朝向(旋转变换)发生改变,而形状不变,得到的变换称为刚性变换。刚性变换是最一般的变换。
平移变换,示意图如下:
旋转变换,示意图如下:
动态磁敏感对比成像
SWI又叫做磁敏感加权成像,最早由E.Mack Haacke等\cite{reichenbach1997small}在1997年发现,当时叫做“高分辨率血氧水平依赖静脉成像”(high resolution blood oxygenation level dependent venographic imaging),至今已经22年,在临床上得到了广泛的应用。
SWI序列基础
SWI根据不同组织间的磁敏感性差异提供图像对比。为了凸显SWI在表现细小静脉及小出血方面的能力,SWI以T2 加权梯度回波序列作为基础进行了改进。与T2 加权梯度回波序列不同的是,SWI采用全流动补偿的梯度回波序列进行扫描,可同时获得幅度图像(magnitude image)和相位图像(phase image)两组图像。
常规MRI仅利用了单一的幅度信息,SWI则利用了一直被忽略的相位信息,并经过一系列后处理将相位图与幅度图融合,形成独特的图像对比。
磁敏感性及常见的磁敏感物质
SWI主要利用组织间磁敏感差异形成图像对比,磁敏感性反映了物质在外加磁场(H)作用下的磁化程度,可以用磁化率(χ)来度量。
人体组织中绝大多数磁敏感改变与血液中铁的不同形式或出血等相关。当血红蛋白中的$Fe^{2+}$与氧结合时,形成的氧合血红蛋白呈反磁性。当氧与铁离子分离形成脱氧血红蛋白时,形成的脱氧血红蛋白有4个不成对电子,呈顺磁性\cite{ogawa1990oxygenation}。
组织内另一种磁敏感的源物质是非血红素铁,它常以铁蛋白的形式存在,表现为反磁性。组织内的钙化通常也呈反磁性,虽然磁敏感效应比铁弱,但也能导致可测量到的敏感性的变化。
无论是顺磁性还是反磁性物质,均可使局部磁场发生变化而引起质子的拉莫尔频率发生变化。如果施加一个足够长的TE,自旋频率不同的质子间将形成明显的相位差别,此时,磁敏感度不同的组织将在SWI相位图上被区分出来。
相位图
与常规磁共振成像不同,相位图反映了质子在弛豫过程中经过的角度(φ),根据磁敏感性的差异反映图像对比,可获得大量反映组织内铁及其他磁敏感性物质含量的信息。
SWI后处理思路
首先去除由于背景磁场不均匀造成的低频扰动,使用一个高通滤波器,滤除低频扰动分量,得到高频分量,即校正后的相位图。
第二步将校正相位图中不同组织的相位值进行标准化处理,建立相位Mask,并将相位Mask与幅度图像多次相乘进行加权。
通常按照下述公式将不同组织的相位值进行标准化处理,得到点x处标准化后的相位值:
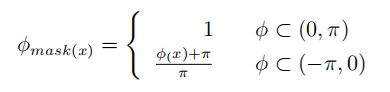
$\phi{x}$代表相位图中点x处的相位,根据公式,相位在$(0,\pi)$的像素,其相位被设定为标准值1,相位在$(-\pi,0)$的像素,其相位值被转化为$(0,1)$,在相位Mask中起到抑制信号的作用。
如公式所示,将$\phi{mask(x)}$做n次幂后与幅度$\rho_(x)$相乘得到SWI图像,n决定了权重的大小。经过相位蒙片与幅度图加权,顺磁性物质的负相位信号得到抑制,在磁敏感加权图像上呈明显的低信号,因此,在失相位区域与正常组织间便形成了较好的对比。
SWI在临床上的应用
SWI利用不同组织间磁敏感的差异成像并将其放大,通过检测病灶中的静脉分布、出血灶和矿物质沉积等,有效改善了相关疾病的诊断,目前主要应用于中枢神经系统。
从SWI原理上可以看到,只要组织间存在磁化率差异,就可以通过SWI显示出组织对比。但由于磁敏感成像对于局部磁场不均匀性特别敏感,因此在某些磁化率差异特别大的区域,其成像却受到一定程度的限制,如颅底的含气鼻窦、脊柱等部位,由于组织间的的磁化率差异极大,因此造成局部特别强的相位伪影。
SWI是MRI常规序列的重要补充,已经成功应用于临床诊断、鉴别诊断及科学研究之中。