本篇博文,主要给大家梳理一下梯度下降算法的发展脉络。
概述
梯度下降的根是随机梯度下降(SGD)算法,后人在SGD的基础上进行了一系列的发展和改进。改进的思路主要有两个:引入动量和自适应学习率。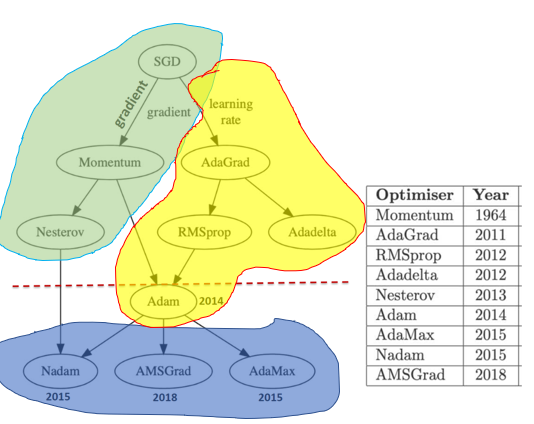
第一章
什么是梯度
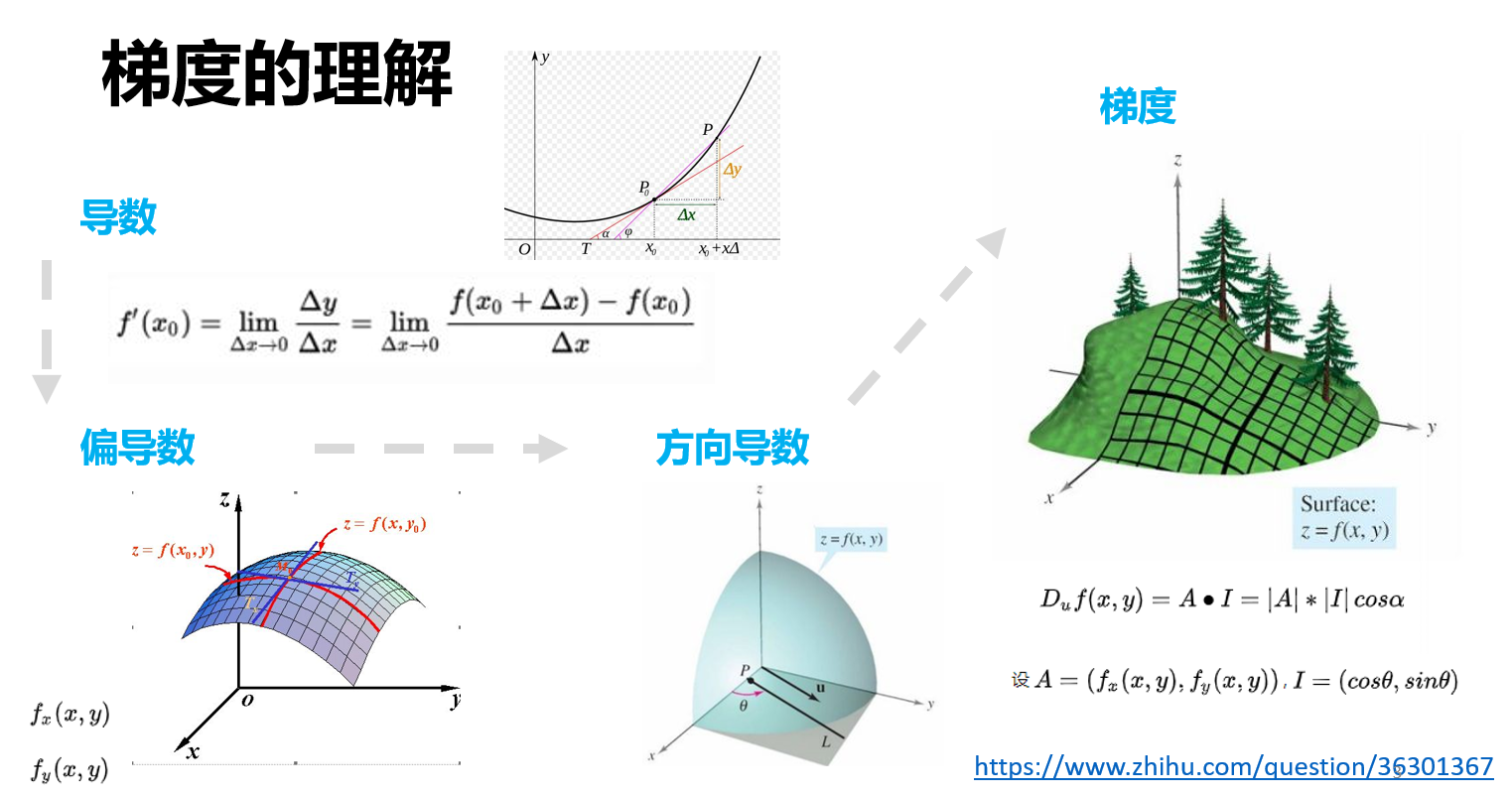
理解梯度之前,我们要理解什么是方向导数;理解方向导数之前,我们需要理解什么是偏导数;理解偏导数之前,我们要对导数有所了解。导数刻画的是函数$f(x)$的变化快慢。偏导数$f_x(x,y)$刻画的是函数$f(x,y)$沿着$x$轴变化的快慢、同理$f_y(x,y)$刻画的是函数$f(x,y)$沿着$y$轴变化的快慢。除了$x$轴、$y$轴之外,如果我们想知道函数沿着方向u的变化快慢怎么办?自然地就引入了方向导数,方向导数刻画的是函数沿着某一个方向变化的快慢。说完方向导数,那什么是梯度呢?梯度就是方向导数最大的那个向量。沿着这个方向,函数变化率最大。
一句话概括,梯度下降法是:沿着梯度反方向更新目标函数$𝑓(\theta)$的参数$\theta$,使目标函数取得极小值的过程。换句话说:在参数的梯度方向上更新参数,使得误差逐渐变小!
梯度下降法的三种变体
Batch gradient descent
这种梯度下降法的特点是,遍历整个训练集的数据后更新一次模型参数$\theta$。因此,这种方法收敛的速度非常慢;如果数据集非常大时,这种训练方法是不可接受的,因为对内存来说是一个非常大的挑战;而且,这种方法不能在线训练网络;
Stochastic gradient descent
SGD的特点是每来一个数据就更新一次$\theta$,所以导致参数更新过于频繁,而且目标函数波动很大。但是它的优点是,可以在线训练。
Mini-batch gradient descent
Mini-batch gradient descent结合了前两者的优点:每次来一个小batch,然后更新一次参数。这样减小了参数更新的方差,使收敛更稳定。值得注意的是:小批量梯度下降法通常也被称为SGD。
梯度下降算法面临的挑战
第一:如何选择合适的学习率是一个令人头疼的问题
选大了,不好收敛;
选小了,收敛太慢;
选个固定的,太蠢了,不能根据数据自适应;(利用查表更新学习率,表的构建也是一个问题)
第二:如何逃脱鞍点?
鞍点的各个方向的梯度都是零
指数加权平均数
介绍动量梯度下降算法之前,有必要给大家介绍一下指数加权平均数。
指数加权算法的核心在于:它对数据进行加权时不是等权重进行的,而是按照指数权重对所有数据进行了加权。这个权重距离t越近,权重越大,反之也越小。
那么,我们为什么要使用加权平均数呢。其实,在训练过程中,数据量是很大的,假设训练样本有100w,即使mini_batch取100,其计算平均值消耗的内存和时间需要的代价都很大,而对于加权平均数,如果β取值0.9那么只需要计算10个数即可计算其平均值,大大节约了内存,计算效率也极大的提高了。
Momentum梯度下降算法
我们知道,普通的梯度下降算法在更新参数时,只考虑了当前的时刻的梯度。加了动量的梯度下降算法,理解起来很简单,在更新模型参数的时候,不仅只考虑了当前时刻的梯度,过去所有时刻的梯度也都考虑进来了,而且,过去时刻的梯度并不是等权重的,是按照指数加权的。离当前时刻的越近,权重越大。
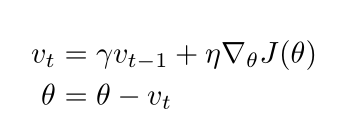
换句话说,其实我们引入动量,就像是将一个球从山上推了下来,在下降的过程中的动量也在不断地增加,这个过程和我们更新参数的过程非常类似。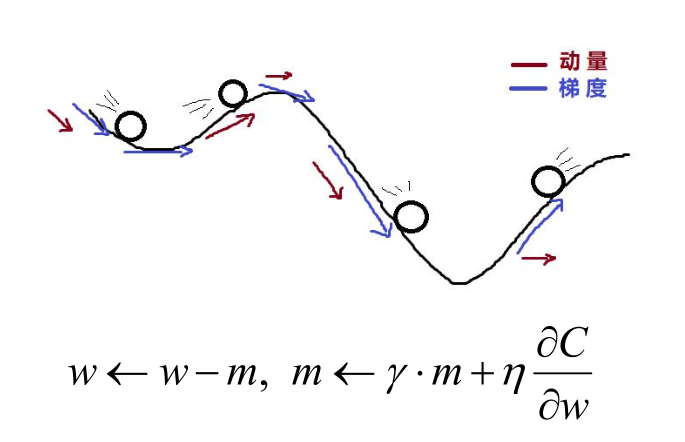
Nesterov Accelerated Gradient梯度下降算法
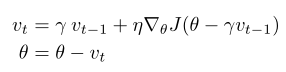
能不能让我们的球在下降的过程中,有点预测能力?答案当然是可以的,既然,我已经知道,我当前时刻$\theta$的更新量是$\gamma*v_{t-1}$,那我为什么还要用现在这个时刻的梯度,我用下一个时刻的梯度不可以吗?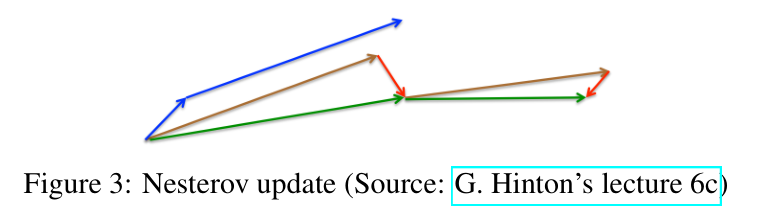
观察上图,我们可以看到:蓝色的短矢量代表当前时刻的梯度、蓝色长矢量代表下一时刻的梯度。当使用NAG算法时,我们使用的是下一时刻的梯度,用棕色的矢量表示,加上之前所有时刻的梯度指数加权的结果:红色的矢量,可以得到当前时刻使用NAG算法更新时的结果:绿色矢量。可以发现,用NAG算法,更新一步所走的步长和SGD走两步差不多。
NAG梯段下降算法是俄罗斯的科学家Nesterov最早提出来的。
小结
SGD看的是现在,加了动量的SGD能够考虑现在和过去;NAG考虑的是下一时刻和过去。
第二章
第一章的落脚点在动量上,第二章节的落脚点就在自适应学习率上。本章主要回答四个问题:AdaGrad和SGD有什么差异,为什么要引入AdaGrad?RMSProp和Adadelta有何异同?Adam结合了什么样的思想,如何结合的?
AdaGrad和SGD有什么差异,为什么要引入AdaGrad?
SGD的学习率是固定的,这意味着,在参数更新的过程中,不管当前的情况如何(梯度大,还是梯度小),更新算法获取信息的能力是固定的。显然这是不合理的,我们希望在梯度大的地方,我们能谨慎一些;在梯度小的地方,也就是平坦的地方,我们能大胆一下。要实现这样的功能,我们的学习率能就要根据实际情况进行变化,这就引入了Adagrad。
如上图所示,Adagrad和SGD的区别在于,Adagrad的学习率是会变的。在梯度大的地方学习率会变小,更新参数时会更谨慎(迈的步子小一些);在梯度小的地方学习率会变大,更新参数时会更大胆些(迈的步子大一些);
Adagrad的优点是:只需给定一个初始的学习率,之后学习率会自适应地调整。但是也有缺点:在分母位置,每次加的都是正数,所以学习率会越来越小,换句话说就是获取知识的能力变得越来越弱。这就引出了下一个方法Adadelta。
Adadelta与Adagrad有何异同?
Adadelta主要解决Adagrad中的两个问题:其一单调递减的学习率、其二需要手工选择一个全局的学习率;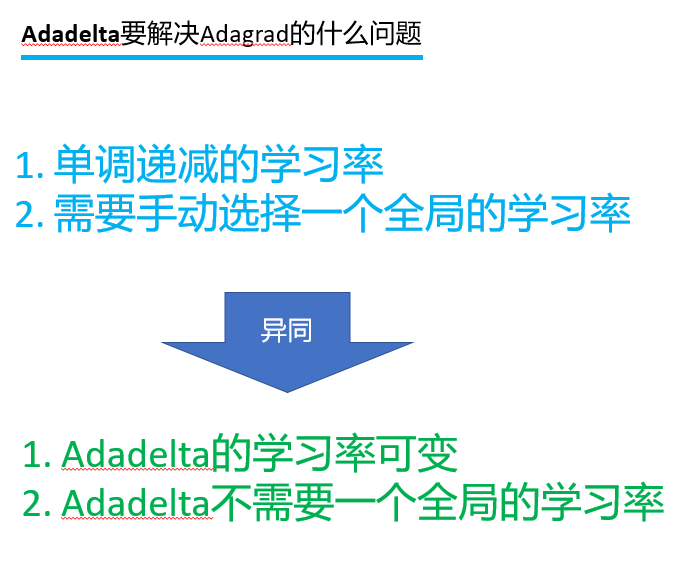
那么如何实现这个想法呢?答案很简单,采用加窗的思想:不是将过去所有的梯度加起来,而是对过去的梯度加了一个时间窗,在窗内的梯度才对我有意义。这样做的好处也很明显了:(1)不像Adagrad那样,梯度会累计到无穷大,而是变成最近梯度的一个局部估计;(2)保证很多次迭代之后,学习率仍然会发生变化(Make Progress)。在实际实现的过程中,使用的正是前文提到的指数加权的形式。
那么对于Adadelta来说,还有一个问题没有解释清楚:Adadelta如何做到不用初始化一个全局学习率的?关于这部分的详细解释,在https://arxiv.org/abs/1212.5701 论文中的第3.2节。我对这一部分的理解是:为什么Adadelta会考虑到这个问题呢?是因为Adadelta的作者发现Adadelta的更新规则和SGD、Momentum相比有些不一样:Adadelta中的学习率是有单位的,而SGD、Momentum是没有单位的,为了使Adadelta也像SGD、Momentum那样:学习率应该是一个无标度的参数。作者把初始化的学习率改成了上一时刻的$\Delta \theta$。用上一个时刻的$\Delta \theta_{t-1}$代替学习率$\eta$。
总结一下Adadelta的优点:自适应学习率,而且不用初始化一个全局的学习率。
RMSProp和Adadelta有何异同?
RMSprop和adagrad的关系:同一时期独立开发的两个算法,都是用来解决Adagrad中学习率大幅度下降的问题。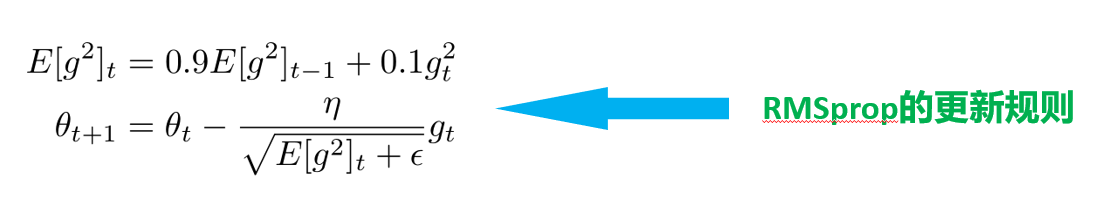
上图是RMSprop的更新规则,可以看到RMSprop和Adadelta的第一步是相同的。
Adam结合了什么样的思想,如何结合的?
第二章的重头戏是Adam,因为它是连连看的典型产物。之前有人在动量上下功夫,又有人在自适应学习率上下功夫,那么下一步呢?肯定有人会想,能不能把两者结合起来呢?答案当然是可以的,Adam也就是这么做的。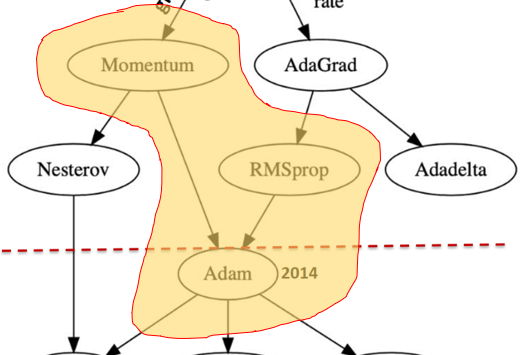
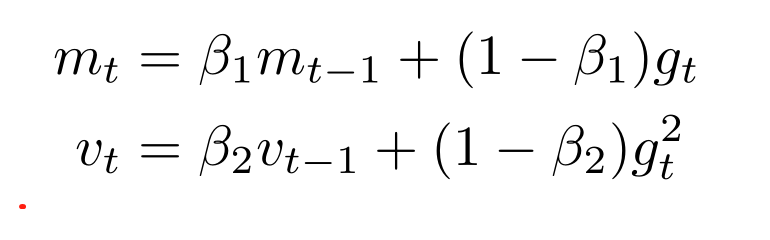
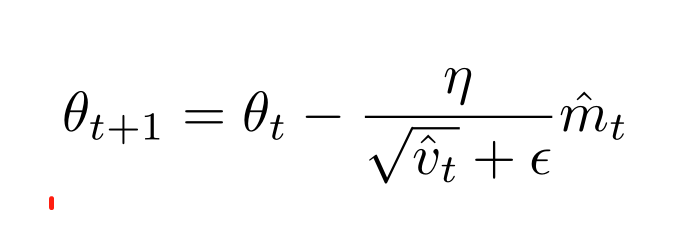
上图是Adam的更新规则,可以看到:Adam不仅引入了动量,而且每一步更新时的学习率也是自适应的。
第三章
第三章的落脚点是针对Adam存在的问题,后人又提出了三种改进的算法。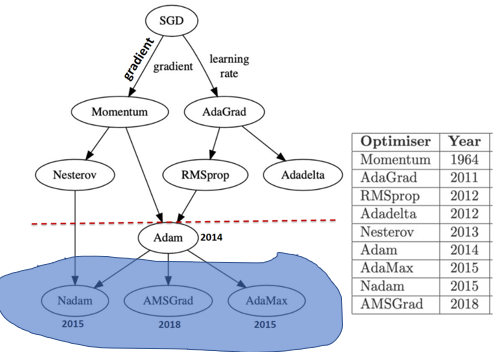
Adam存在两个比较突出的问题
第一点:Adams可能不收敛。为什么不收敛,因为Adam阶动量是固定时间窗口内的累积,随着时间窗口的变化,遇到的梯度可能变化特别大,因此会导致震荡不收敛。
第二点:Adams会错失全局最优解;有文献[The marginal value of adaptive gradient methods in machine learning]报道,同样的一个优化问题,不同的优化算法可能会找到不同的答案,但自适应学习率的算法(Adam)往往找到非常差的答案。
Adamax
Adamax是Adam那篇文献中的一个讨论。文章中提到,能不能把二阶范数改成无穷阶范数呢?因为作者在数学上证明了无穷阶范数也是收敛的。
从这个角度看,Adamax和Adam唯一的区别就在学习率上。
Nadam
介绍Nadam之前,我们需要回顾一下NAG算法。因为,Nadam借鉴了NAG中的思想:不只看眼前,我要看远点,看下一个时刻。NAG中看远点看的是下一时刻的梯度,Dozat对这一点进行了小小个更新,他把NAG的更新规则修改为如下的方式: 
如何理解呢?可以这样:NAG是用梯度向前看,Dozat想用动量向前看。很自然地,我们就得到了Nadam的更新规则,如公式33所示,把$m_{t-1}$换成了下一时刻的动量$m_t$。
AMSGrad
AMSGrad和Adam最大的区别在于,AMSGrad用的是过去所有所有$v_{t}$中最大的那个$v_t$,这样就会避免掉入$v_t$不断增长的陷阱中。因$v_t$不断增长会导致学习率不断下降,从而收敛的速度会变得非常慢。
下图是AMSGrad的更新规则:
如下图所示,是Adam和AMSGrad收敛速度的比较,可以看到,在作者的实验中,AMSGrad比Adam有着更高的收敛速度和稳定性。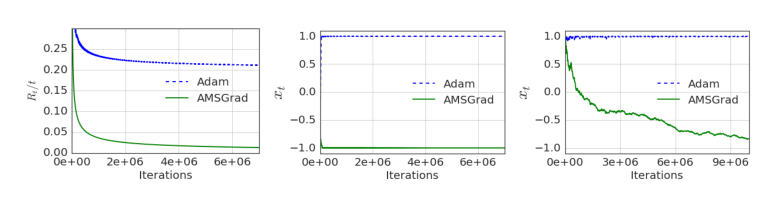
总结
以上三章,我详细地梳理了梯度下降算法的发展脉络。通过梳理,我发现,连连看的思想无处不在,当人们意识到固定的学习率很糟糕是就会像能不能自适应呢?实现了自适应之后,人们又会想能不能把动量和自适应学习率放在一起呢,于是就有了Adam。后来人们又看了Adam的缺点,能不能让它收敛地更稳健一些呢,于是就有了Adam的各种改进版本。