变分模态分解其实是经验模态分解EMD的一种扩展。
虽然EMD能够结合信号本身的特点分解出多个模态函数IMF,但是它也存在一些缺点:
首先:EMD对噪声敏感,怎么理解呢?在进行EMD分解时,我们需要利用信号的极大值和极小值来计算包络,而信号的极值很有可能收到噪声干扰,因此EMD对噪声比较敏感。
其次,EMD分解存在端点效应,什么是端点效应呢?端点效应指的是在信号的端点处,由于没有前后帧的信息,求得的包络面可能不准确,在后期分解的过程中,可能会得到不准确的IMF分量。
最后,EMD是经验模态分解,它很多时候依赖的是经验,数学基础还不完善。
今天给大家介绍的变分模态分解分解VMD,相较于EMD抗噪能力更好,它是怎么做的呢?它有一个基本假设,它假设信号都能够分解成若干个经过调频和调幅信号的叠加。换句话说,一个信号$f(t)$,其实是由若干个具有不同中心频率和一定带宽信号的叠加。这是VMD分解的重要假设。
接下来,我们看VMD是怎么进行分解的:VMD把分解过程转换成了一个优化问题,优化什么了,刚才说过,信号$f(t)$,是由若干个具有不同中心频率和一定带宽信号的叠加。VMD优化的是让这些不同中心频率的信号的带宽尽可能的窄,窄有什么意义呢?我们可以想一个极端的情况,如果信号的带宽窄成只有一个频率分量,那不就是$cos$函数了嘛。这么时候VMD分解说的就是,把原始信号$f(t)$分解成若干个不同中心频率$cos$函数。
公式14说的就是优化问题,这是一个典型的病态问题,要想解决这个病态问题,我们必须要引入$\lambda$,拉格朗日惩罚因子;看公式15,它说的是,首先,我想让的IMF分享的带宽尽可能的窄,同时,还让是的我分解之后的分量重建回去要和原始信号尽可能的像,最后还要根据信号的噪声水平引入惩罚项,对噪声进行惩罚。
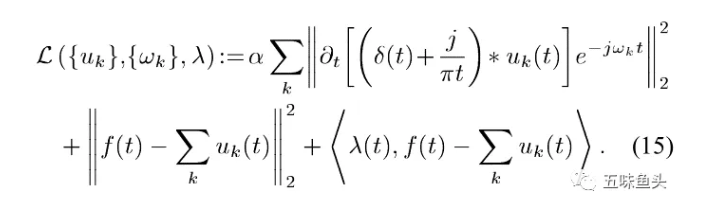
结合以上三方面的考虑,我们就能够求解出来这个问题了,
以上就是VMD,变分模态分解最核心的内容。
最后,是VMD分解的局限性,到底能分解出来几个分量,这个参数k是由用户提前给定的。给的不好,分解出来的结果也不好。
以上就是今天分享的全部内容。