对Snake模型的理解和认识

首先对问题进行抽象，然后得到模型，最后求解。

Snake模型的起源

Marr教授提出的视觉理论认为：视觉处理任务是一个仅依赖图像底层结构而不需要使用高层知识的过程。然而，Kass等并不认同这种理论，他认为图像处理是一个整体的行为，底层信息的处理必定要依赖于高层信息。为了将两个层面的信息融于一体，他们试图通过叠加的方式构造这样的能量函数：包括内部能量、外部能量、图像能量等多种可供用户选择或定义的能量项。在这一思想的指导下，Kass等于1987年提出了著名的Snake模型，也称为活动轮廓模型。Snake模型是定义在图像内能够在内部力和外部力作用下移动的曲线，属于可形变模型的一种。

Snake模型的变种

名称	提出者	年代
基本Snake	Kass M	1988
Balloon Snake	Cohen L D	1991
梯度矢量流	Xu Cheng-yang	1997
几何活动轮廓	Kichenassamy S	1993
测地线模型	Caselles V	1997
水平集	Osher S	1988/1996
变分水平集	Zhao Hong-kai	1996
动态规划	Amini A	1990
贪婪算法	Williams D	1992

基础知识

变分的概念

一言以蔽之，泛函是函数的函数，对于泛函的微分就是变分。

Euler-Lagrange方程

Snake模型给出了一个能量泛函，采用变分法可以求得泛函极值（实际上，目前只有7个泛函存在解析解）。获得目标轮廓的过程实际上就是求泛函极值的过程。泛函极值解对应的方程是Euler-Lagrange方程，如下：

$$F_y-\ \frac{d}{dx}F_y=0$$

或者表示为

$$F_y-F_{xy^\prime}-F_{yy^\prime}-F_{yy}y^{\prime\prime}=0$$

梯度下降法

我们知道Snake模型中的轮廓线并不是连续的，而是一组离散的数值。而Euler-Lagrange存在解析解的必要条件是$y(x)$必须连续可微的。而Snake模型中的轮廓线并不满足这一点，所以，我们只能通过最优化方法求解。
以一维能量泛函为例，其能量泛函形式为：

$$E\left(u\right)=\int_{x_0}^{x_1}{F(x,u,u_x)dx}\$$

其中函数$u(x)$满足固定条件$u(x_0)\ =\ a,u(x_1)\ =\ b$，于是$E(u)$的极值对应于变分：

$$\frac{\partial E}{\partial u}=0$$

我们考虑将$u\left(x\right)+v(x)$作为最优解$u\left(x\right)$的微扰。当$v(x)$和$v^\prime(x)$足够小时，由Taylor展开得到：

$$F\left(x,u+v,u^\prime+v^\prime\right)=F\left(x,u,u^\prime\right)+\frac{dF}{du}v+\frac{dF}{dv}u+\ldots$$

于是有

$$E\left(u+v\right)=E\left(u\right)+\int_{x_0}^{x_1}\left(v\frac{\partial F}{\partial u}+v^\prime\frac{\partial F}{\partial u^\prime}\right)dx$$

根据分部积分法，可以推得，当$u$达到稳定解时，即对应能量泛函的极小值：

$$\frac{\partial u}{\partial t}=0\Longrightarrow\ \frac{\partial F}{\partial u}-\frac{d}{dx}\left(\frac{\partial F}{\partial u_x}\right)-\frac{d}{dx}\left(\frac{\partial F}{\partial u_y}\right)=0$$

曲线演化理论

在二维空间$R^2$中，曲线演化可描述为以时间为变量的一条光滑闭合的曲线沿着其法线方向以一定速度运动的过程，用于图像分割中的曲线演化。假设二维参数化曲线$C(p)\ =\ (x(p),y(p))$，其中p为曲线的参数。在Snake模型中，我们使用弧长参数对曲线进行描述。

Snake模型推导

Snake曲线是由一组轮廓点 $v\left(s\right)=v\left[x\left(s\right),y\left(s\right)\right],s\in(0,1)$组成的参数曲线。通过构造能量函数

$$E_{Snake}=\ E_{internal}+E_{external}+E_{constraint}$$

其中$E{Snake}$为总能量，$E{internal}$为内部能量，内部能量存在的意义是约束曲线的性质，如曲线的弹性、光滑性。$E{external}$为外部能量，一般考虑图像的整体信息，一般外部能量达到最小值时轮廓线运动到图像梯度最大的地方。$E{constraint}$一般为用户指定的其他约束条件。

内部能量为：

$$E_{internal}\left(v\left(s\right)\right)=\ \alpha E_{spring}+\beta E_{smoothness}=\alpha\left|\frac{dv}{ds}\right|^2+\beta\left|\frac{d^2v}{ds^2}\right|^2$$

内部能量包括弹性能量$E{spring}$和光滑性能量$E{smoothness}$。
弹性能量表示为：

$$E_{spring}=\ \alpha\left|\frac{dv}{ds}\right|^2$$

弹性能量使得snake曲线不断收缩；曲线越长，曲线对弧长参数的一阶导数幅值就越大。

光滑性能量表示为:

$$E_{smoothness}=\ \beta\left|\frac{d^2v}{ds^2}\right|^2$$

光滑性能量使得Snake曲线像薄板一样运动，曲线越尖锐，二阶导数的幅值越大。
在能量最小化的过程中，一阶导数保证Snake曲线收缩，二阶导数保证Snake曲线光滑。$\alpha$和$\beta$两个参数分别代表两项的权重，$\alpha$权值越大曲线收缩的越快，$\beta$权值越大曲线越光滑。

外部能量$E_{external}$，通常要考虑图像的整体信息。Kass等采用图像的梯度作为外部能量。在外部能量的驱使下，Snake模型会往图像梯度最大的方向运动。
外部能量定义如下：

$$E_{external}=\ \gamma\ E_{image}=\ -\gamma\left|\nabla I\right|^2$$

综上所述总能量$E_{snake}$表示为：

$$E_{snake}=\ \int_{0}^{1}\left[\alpha E_{spring}+\beta E_{smoothness}+\gamma E_{images}\right]ds\$$

使用变分法进行求解

首先给出能量泛函，能量泛函极值对应的解，就是目标轮廓

$$E_{snake}=\ \int_{0}^{1}\left[\alpha E_{spring}+\beta E_{smoothness}+\gamma E_{images}\right]ds$$

根据泛函极值存在的必要条件给出欧拉-拉格朗日方程

$$\alpha v_{ss}-\beta v_{ssss}-\ \nabla E_{image}=0$$

由于欧拉-拉格朗日方程存在解析解的必要条件是函数必须要连续，而轮廓线是离散的，因此针对Snake模型构造的欧拉-拉格朗日方程不存在解析解。我们只能采用最优化方法逼近最优解，迭代方程如下：

$$V_{j+1}=\ M^{-1}(V_j-E_{images})$$

分割效果

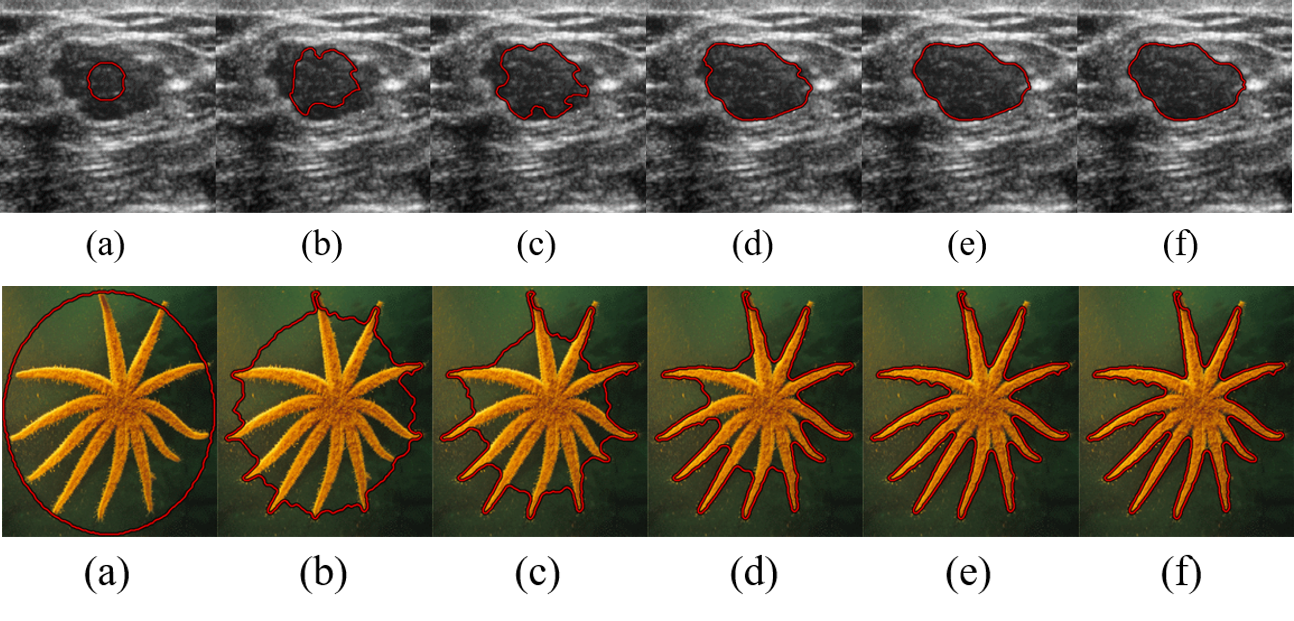
小结

Snake模型中三个参数$\alpha$、$\beta$和$\gamma$的设置没有固定的标准或统一的规则，一般通过经验来调整和实践结果反复来调整。基于Snake模型的图像分割方法具有结合高层先验知识与底层局部结构的特点，适用于目标轮廓光滑的场景，但它也存在不足，表现在分割过程中，无法改变自身拓扑结构方面，无法收敛到凹陷区域以及对初始轮廓线的位置比较敏感，而且需要给定一个初始的轮廓线。