思想:在不同尺度空间上寻找特征点,并加以描述
问题链
- 什么是SIFT?
- 为什么要提出来这种方法,解决什么问题?
- 这个方法的思想是什么?
- 方法的具体内容有哪些?
- 前提是什么?局限性有哪些?
- 效果怎么样?
什么是SIFT?
1999年British Columbia大学大卫.劳伊(David G.Lowe)教授提出了一种基于尺度空间的、对图像缩放、旋转甚至仿射变换保持不变性的图像局部特征描述算子-SIFT(尺度不变特征变换),这种算法在2004年被加以完善。
为什么要提出来这种方法,解决什么问题?
在目标检测领域,识别杂乱的真实场景中的物体是一个很困难的任务,需要找到一些不受遮挡、光照、变形等因素影响的特征点。传统的方法如角点、边缘检测,鲁棒性、适应性差。
Lowe提出来的SIFT方法一定程度上能够解决这些问题:在图像上寻找一些特殊的特征点,这些特征点对光照、仿射变换具有一定程度的不变性,因此可以拿来做特征匹配,目标识别。
这个方法的思想是什么?
在不同尺度空间上寻找具有方向信息的局部极值点作为特征点。
方法的具体内容有哪些?
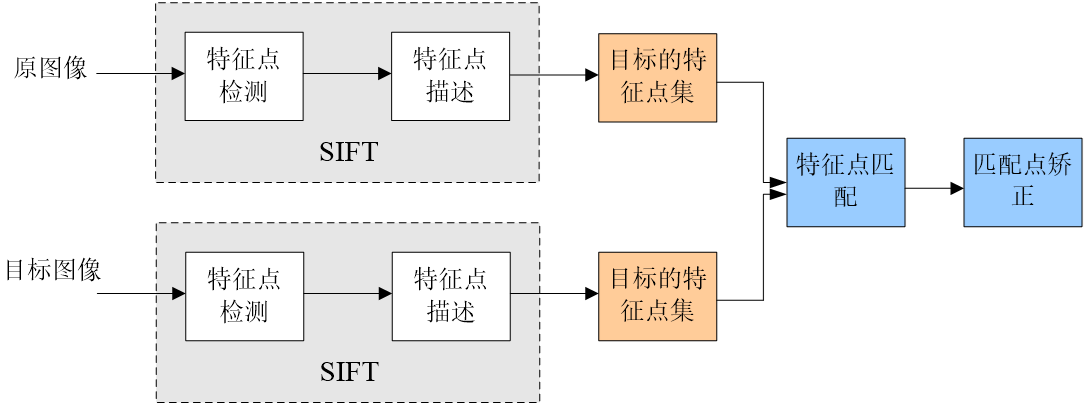
SIFT算法实现物体识别主要有三大工序:
- 提取关键点;
- 对关键点进行描述,生成关键点的描述器;
- 关键点匹配,通过两方特征点的两两比较找出相互匹配的若干对特征点,也就建立了景物间的对应关系。
什么是尺度空间?如何构造
尺度空间是用来模拟人在距离目标由近到远时,目标在视网膜上的投影情况。尺度是自然存在的,不是人为创造的。在数学上,可以利用不同大小的高斯卷积核来描述不同的尺度空间。
高斯核:
和高斯核卷积后的图像:
高斯金字塔
高斯金子塔的构建过程可分为两步:
- 对图像做高斯平滑;
- 对图像做降采样。
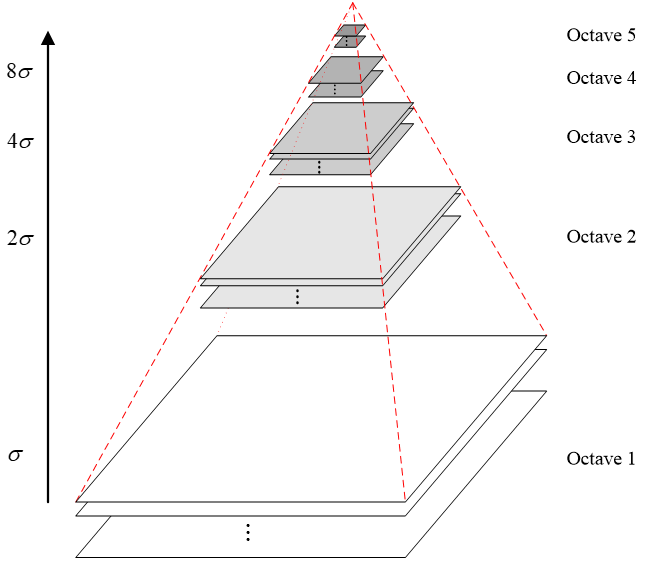
为了让尺度体现其连续性,在简单下采样的基础上加上了高斯滤波。一幅图像可以产生几组(octave)图像,一组图像包括几层(interval)图像。
如何寻找特征点?
所有特征点的检测都是基于尺度不变的特性。Lindeberg[Lindeberg, Tony, “Scale-space theory: A basic tool for analysing structures at different scales”, Journal of Applied Statistics, 21, 2 (1994), pp. 224–270.]指出尺度规范化的LoG算子具有真正的尺度不变性。
LoG算子即(Laplacion of Gaussian),可以由高斯函数梯度算子GOG构建。
尺度规范化的GoG算子:
尺度规范化的LoG算子:
高斯差分算子
LOG算子与高斯核函数的关系如下:
通过推导可以看出,LOG算子与高斯核函数的差有直接关系,由此引入一种新的算子DOG(Difference of Gaussians),即高斯差分算子。高斯差分算子(DoG)能够近似代替拉普拉斯高斯算子(LoG)[Mikolajczyk K., Schmid C. (2002) An Affine Invariant Interest Point Detector. ]
构建高斯差分金字塔
对应DoG算子,我们要构建DOG金字塔: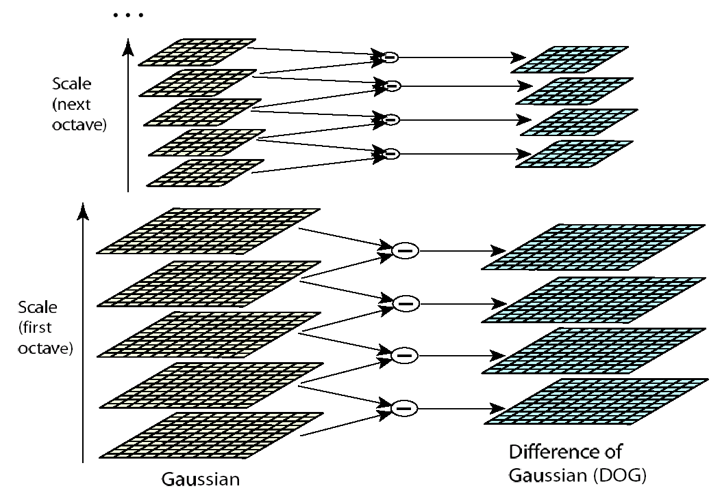
我们可以通过高斯差分图像看出图像上的像素值变化情况。如果没有变化,也就没有特征。特征必须是变化尽可能多的点。DoG图像描绘的是目标的轮廓。
DoG局部极值检测
关键点是由DOG空间的局部极值点组成的。为了寻找DoG函数的极值点,每一个像素点要和它所有的相邻点比较,看其是否比它的图像域和尺度域的相邻点大或者小。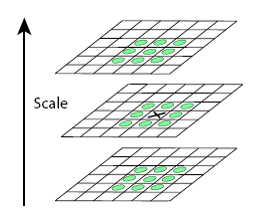
中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2个点共26个点比较,以确保在尺度空间和二维图像空间都检测到极值点。
关键点精确定位
为了提高关键点的稳定性,需要对尺度空间DoG函数进行曲线拟合。利用DoG函数在尺度空间的Taylor展开式:
其极值点为:
关键点方向分配
通过尺度不变性求极值点,可以使其具有缩放不变的性质,利用关键点邻域像素的梯度方向分布特性,我们可以为每个关键点指定方向参数,从而使描述子对图像旋转具有不变性。
我们通过求每个极值点的梯度来为极值点赋予方向。
像素点的梯度表示:
梯度幅值:
梯度方向:
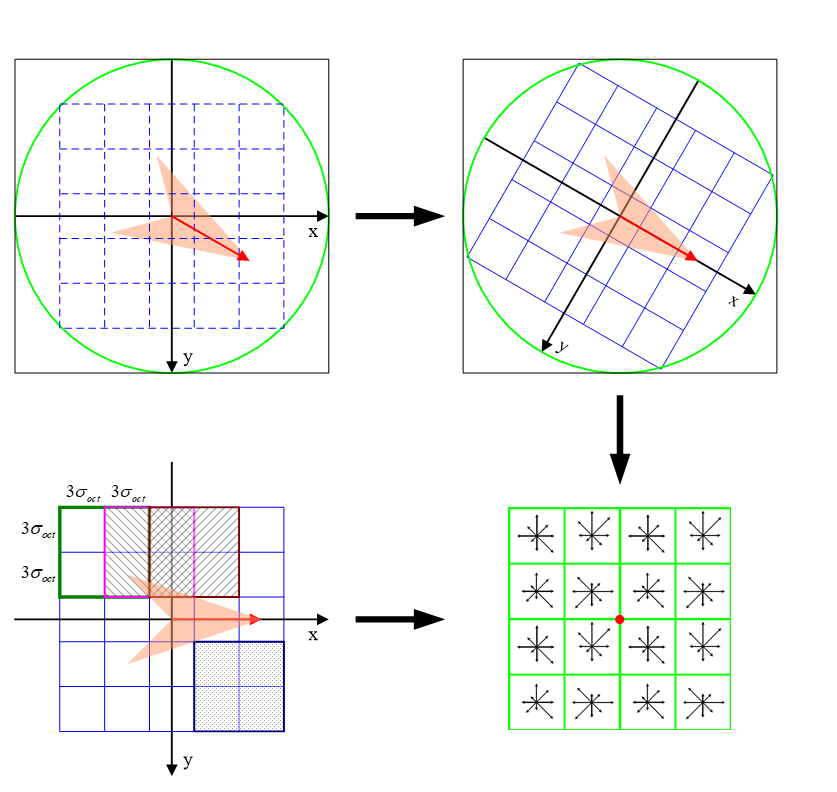
确定关键点的方向时采用直方图统计法,统计以关键点为中心,一定区域内的梯度分布情况。
- 直方图以每10度方向为一个柱,共36个柱,柱所代表的方向为像素点梯度方向,柱的长短代表了梯度幅值。
- 根据Lowe的建议,直方图统计半径采用$3 \ast 1.5 \ast \sigma$。
- 在直方图统计时,每相邻三个像素点采用高斯加权,根据Lowe的建议,模板采用[0.25,0.5,0.25],并连续加权两次。

如何对关键点描述?

图像的关键点已检测完毕,每个关键点有三个信息:位置、尺度、方向;同时也就使关键点具备平移、缩放、和旋转不变性。
描述的目的
描述的目的是在关键点计算后,用一组向量将这个关键点描述出来,这个描述子不但包括关键点,也包括关键点周围对其有贡献的像素点。用来作为目标匹配的依据,也可使关键点具有更多的不变特性,如光照变化、3D视点变化等。
描述的思路
通过对关键点周围图像区域分块,计算块内梯度直方图,生成具有独特性的向量,这个向量是该区域图像信息的一种抽象,具有唯一性。
关键点描述
下图是一个SIFT描述子事例。其中描述子由2×2×8维向量表示,其实也是2×2个8方向的直方图。左图的种子点由8×8单元组成。每一个小格都代表了特征点邻域所在的尺度空间的一个像素,箭头方向代表了像素梯度方向,箭头长度代表该像素的幅值。然后在4×4的窗口内计算8个方向的梯度方向直方图。绘制每个梯度方向的累加可形成一个种子点,如右图所示:一个特征点由4个种子点的信息所组成。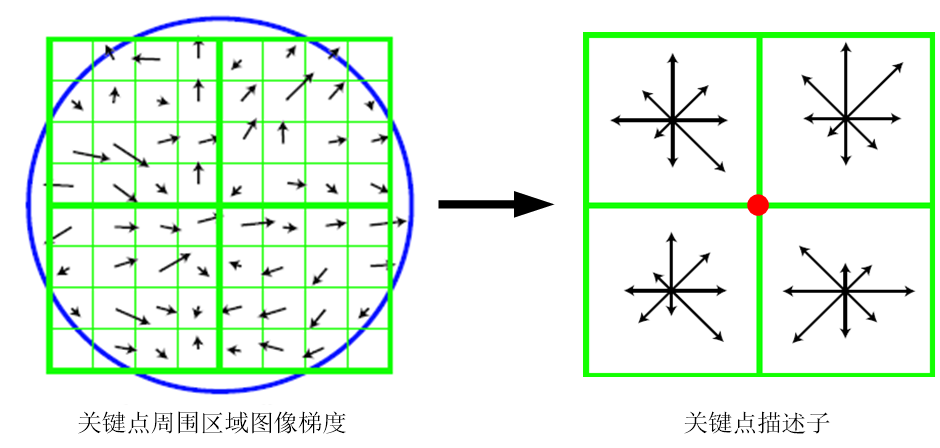
Lowe实验结果表明:描述子采用4×4×8=128维向量表征,综合效果最优(不变性与独特性)
描述子向量元素规范化:
规范化后的向量:
利用关键点进行匹配?
常见的方法是用穷举法: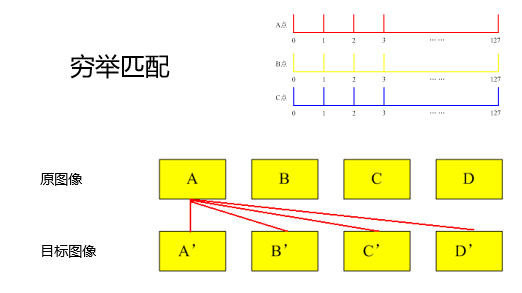
前提是什么?局限性有哪些?
三个前提:
- 一定程度的尺度不变性;
- 图像要发生变化,否则就没有意义;
- 对于局部的运动要一致,否则该方法不适用;
SIFT在图像的不变特征提取方面拥有无与伦比的优势,但其并不是完美的,仍然存在着实时性不高、有时特征点较少、对边缘模糊的目标无法准确提取特征点等缺陷。自从1999年,SIFT算法问世以来,人们从未停止对它的优化和改进。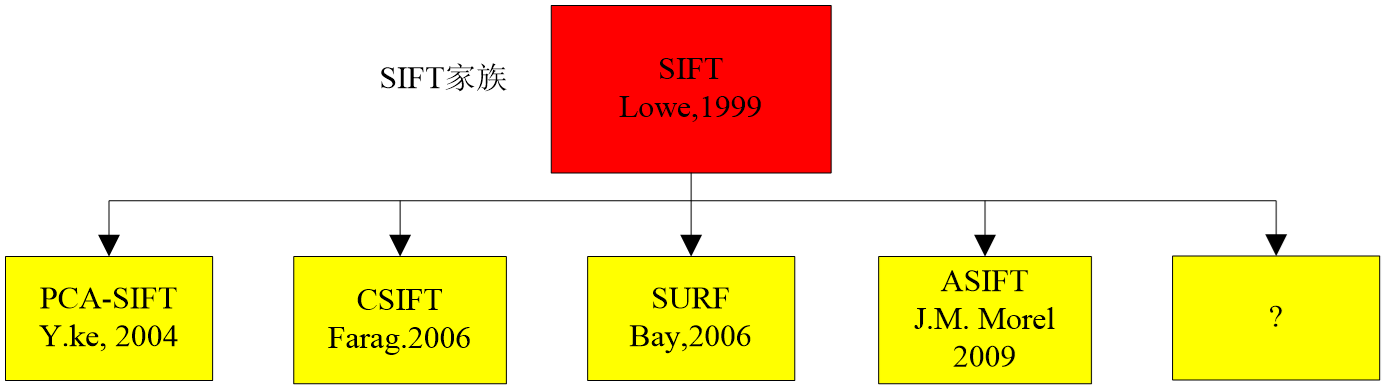
效果怎么样?

Souce Code
souce code:
http://www.cs.ubc.ca/~lowe/keypoints/siftDemoV4.zip
description
https://www.cs.ubc.ca/~lowe/keypoints/